题目内容
如图，?ABCD的对角线AC、BD相交于点O，则下列条件中不能判定四边形ABCD为矩形的是（ ）| A、AB=AD |
| B、OA=OB |
| C、AC=BD |
| D、DC⊥BC |
考点：平行四边形的性质
专题：
分析：根据矩形的判定定理：有一个角是直角的平行四边形是矩形，对角线相等的平行四边形是矩形分别进行分析即可．
解答：解：A、不能判定四边形ABCD为矩形，故此选项符合题意；
B、由AO=BO可证明AC=BD，能判定四边形ABCD为矩形，故此选项不符合题意；
C、AC=BD能判定四边形ABCD为矩形，故此选项不符合题意；
D、DC⊥BC能判定四边形ABCD为矩形，故此选项不符合题意；
故选：A．
B、由AO=BO可证明AC=BD，能判定四边形ABCD为矩形，故此选项不符合题意；
C、AC=BD能判定四边形ABCD为矩形，故此选项不符合题意；
D、DC⊥BC能判定四边形ABCD为矩形，故此选项不符合题意；
故选：A．
点评：此题主要考查了矩形的判定，关键是熟练掌握矩形的判定定理．
练习册系列答案
新编小学单元自测题系列答案
字词句段篇系列答案
相关题目
如图，AD∥BC，∠A是∠ABC的2倍，
如图，直线y=kx+b与x轴相交于点（-4，0），则y＜0时，x的取值范围是（ ）| A、x＜-4 | B、x＞0 |
| C、x＞-4 | D、x＜0 |
如图，用8块相同的长方形地砖拼成一个大长方形，则每个长方形地砖的面积是（ ）| A、200cm2 |
| B、300cm2 |
| C、600cm2 |
| D、2400cm2 |
若a＞b，则下列不等式正确的是（ ）
| A、2a＜2b | ||||
| B、a-2＞b-2 | ||||
C、-
| ||||
| D、a-b＜0 |
若不等式组2＜x＜a的整数解恰有3个，则a的取值范围是（ ）
| A、a＞5 | B、5＜a＜6 |
| C、5≤a＜6 | D、5＜a≤6 |
若（x-3）0-2（3x-6）-2有意义，则x的取值范围是（ ）
| A、x＞3 |
| B、x≠3且x≠2 |
| C、x≠3或x≠2 |
| D、x＜2 |
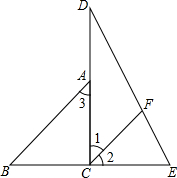将一副三角板拼成如图的图形，其中CD⊥BE于点C，∠D=30°，∠B=45°，且过点C作CF平分∠DCE交DE于点F．