题目内容
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,AF⊥BD,CE⊥BD,垂足分别为E、F;连结AE、CF,得四边形AFCE,试判断四边形AFCE是下列图形中的哪一种?①平行四边形;②菱形;③矩形;请证明你的结论.

平行四边形;证明见解析.
【解析】
试题分析:(1)四边形AFCE为平行四边形;
(2)可先证明△AOF≌△COE,可得OF=OE,又有OA=OC,根据对角线互相平分的四边形是平行四边形,可得四边形AFCE是平行四边形.
试题解析:(1)【解析】
画图连接AE、CF,
四边形AFCE为平行四边形.

(2)证明:∵AF⊥BD,CE⊥BD,
∴∠AFO=∠CEO.
又∵∠AOF=∠COE,
∴OA=OC.
∴△AOF≌△COE(AAS),
∴OF=OE.
又∵OA=OC,
∴四边形AFCE是平行四边形.
考点:1.平行四边形的判定与性质;2.全等三角形的判定与性质.

练习册系列答案
相关题目
若△ABC∽△A′B′C′,相似比为1:2,则△ABC与△A′B′C′的面积的比( )
| A.1:2 | B.2:1 | C.1:4 | D.4:1 |

 的一个根是0.则a的值为( ).
的一个根是0.则a的值为( ).

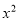 +bx+c的图象经过A(-1,0)和B(3,0)两点,且交
+bx+c的图象经过A(-1,0)和B(3,0)两点,且交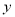 轴于点
轴于点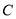 .
.
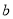 、
、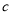 的值;
的值;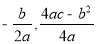 )
)