题目内容
2.有一群猴子,一天结伴去偷桃子.分桃子时,如果每只猴子分3个,那么还剩下59个,如果每个猴子分5个,就都分得桃子,但有一个猴子分得的桃子不够4个.你能求出有几只猴子,几个桃子吗?分析 设有x只猴子,则有(3x+59)个桃子,根据桃子所剩的数量作为不等关系可列不等式:0<(3x+59)-5(x-1)<4,解之可得解集,取整数解即可.
解答 解:设有x只猴子,则有(3x+59)个桃子,
根据题意得0<(3x+59)-5(x-1)<4
解得:29.5<x<32,
∵x为正整数,
∴x=30或x=31,
当x=30时,3x+59=149;
当x=31时,3x+59=152;
答:有30只猴子,149个桃子或有31只猴子,152个桃子
点评 本题考查一元一次不等式组的应用,将现实生活中的事件与数学思想联系起来,读懂题列出不等式关系式即可求解.

练习册系列答案
相关题目
13.顶点是(2,-1)的抛物线的表达式是( )
| A. | y=-(x-2)2-1 | B. | y=(x+2)2-1 | C. | y=3(x-2)2+1 | D. | y=2(x-1)2+1 |
10.将代数式x2-2x+2化为(x+p)2+q的形式,正确的是( )
| A. | (x-1)2-3 | B. | (x-1)2+1 | C. | (x+1)2+2 | D. | (x+1)2+1 |
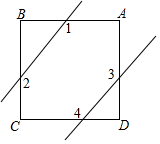 如图,正方形ABCD中,截去∠B、∠D后,∠1、∠2、∠3、∠4的和为540°.
如图,正方形ABCD中,截去∠B、∠D后,∠1、∠2、∠3、∠4的和为540°.