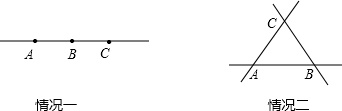题目内容
平面内有三点A、B、C,过其中任意两点画直线,有如下两种情况:(1)若平面内有四个点A、B、C、D,过其中任意两点画直线,有多少种情况?请画图说明;
(2)若平面内有6个点,过其中任意两点画直线,最多可以画多少条直线?
(3)若平面内有n个点,过其中任意两点画直线,最多可以画多少条直线?(直接写出结果)
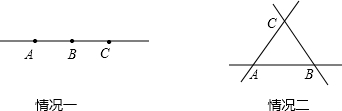
分析:(1)四个点共线,其中三点共线,任意三点不共线3种情况讨论,作出图形可得答案;
(2)当平面内有6个点,当任意三点不共线时,可以作出最多的直线条数;分析可得答案;
(3)由(2)的结论可知,当平面的点数由n增加1变为(n+1)时,可作出的直线数增加n.故可得答案.
(2)当平面内有6个点,当任意三点不共线时,可以作出最多的直线条数;分析可得答案;
(3)由(2)的结论可知,当平面的点数由n增加1变为(n+1)时,可作出的直线数增加n.故可得答案.
解答:解:(1)

(2)最多可画:1+2+3+4+5=15(条);
(3)最多可画:1+2+3+…+n=
(条).

(2)最多可画:1+2+3+4+5=15(条);
(3)最多可画:1+2+3+…+n=
| n(n-1) |
| 2 |
点评:此类题没有明确平面上三条不重合直线的相交情况,需要运用分类讨论思想,解答时要分各种情况解答,要考虑到可能出现的所有情形,不要遗漏,否则讨论的结果就不全面.

练习册系列答案
相关题目
 平面内有三点
平面内有三点 平面内有三点
平面内有三点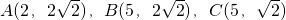 .
.