题目内容
6.若m、n是关于x的一元二次方程x2-8x+15=0的两个实数根,其中m<n,当m<x<n时,化简:$\sqrt{{x}^{2}-10x+25}$+|3-x|( )| A. | 2 | B. | -2 | C. | 2x-2 | D. | 2x+2 |
分析 利用因式分解法解得这个一元二次方程的两个根,然后再根据x的取值范围并利用二次根式的性质来化简原式从而得到答案.
解答 解:∵方程x2-8x+15=0的两个实数根,
∴此方程的两根分别为:x1=3,x2=5,
∵m、n是关于x的一元二次方程x2-8x+15=0的两个实数根,其中m<n,
∴m=3,n=5,
∵m<x<n,
∴3<x<5,
∴3-5<x-5<5-5,即-2<x-5<0,
3-3>3-x>3-5,即0>3-x>-2,
∴原式=$\sqrt{(x-5)^{2}}$+|3-x|=-(x-5)-(3-x)=2,
故选:A.
点评 本题主要考查了因式分解法解一元二次方程以及二次根式的化简的性质与化简的知识,解答本题的关键是求出m和n的值,此题难度不大.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
17. 如图,能判定EB∥AC的条件是( )
如图,能判定EB∥AC的条件是( )
 如图,能判定EB∥AC的条件是( )
如图,能判定EB∥AC的条件是( )| A. | ∠C=∠1 | B. | ∠A=∠2 | C. | ∠C=∠3 | D. | ∠A=∠1 |
18.某商品的标价为132元,若以9折出售仍可获利10%,则此商品的进价为( )
| A. | 88元 | B. | 98元 | C. | 108元 | D. | 118元 |
16.如果点P(-4,y)在第二象限,则y的取值范围是( )
| A. | y>0 | B. | y<0 | C. | y≥0 | D. | y≤0 |
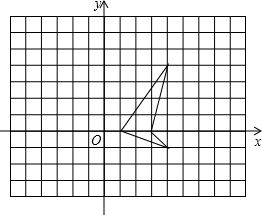 如图,方格纸中有一条可爱美丽的小金鱼
如图,方格纸中有一条可爱美丽的小金鱼