题目内容
 某中学要在教学楼后面的空地上用40米长的竹篱笆围成一个矩形ABCD,将此矩形地块作为生物园,矩形的一边AD用教学楼的外墙,其余三边用竹篱笆,设矩形的边AB(AB<AC)为x米,面积为y平方米.
某中学要在教学楼后面的空地上用40米长的竹篱笆围成一个矩形ABCD,将此矩形地块作为生物园,矩形的一边AD用教学楼的外墙,其余三边用竹篱笆,设矩形的边AB(AB<AC)为x米,面积为y平方米.(1)求S与x之间的函数关系式并求出x的自变量取值范围;
(2)若生物园的面积为150平方米,请求出此时BC的长.
考点:一元二次方程的应用,根据实际问题列二次函数关系式
专题:几何图形问题
分析:(1)设矩形的边AB为x米,则边BC为40-2x米,根据矩形面积公式“面积=长×宽”列出函数的关系式.
(2)令y=150,求出方程-2x2+40x=150求解即可.
(2)令y=150,求出方程-2x2+40x=150求解即可.
解答:解:(1)设矩形的边AB为x米,则边BC为40-2x米,
y=x(40-2x)=-2x2+40x,
又要围成矩形(AB<AC),
则40-2x≥x,x≤
.
x的取值范围:0<x≤
;
(2)令y=150,则-2x2+40x=150,
即x2-20x+75=0,
解得x1=15(不合题意舍去),x2=5,
40-2x=40-10=30.
则BC的长为30米.
y=x(40-2x)=-2x2+40x,
又要围成矩形(AB<AC),
则40-2x≥x,x≤
| 40 |
| 3 |
x的取值范围:0<x≤
| 40 |
| 3 |
(2)令y=150,则-2x2+40x=150,
即x2-20x+75=0,
解得x1=15(不合题意舍去),x2=5,
40-2x=40-10=30.
则BC的长为30米.
点评:考查了一元二次方程的应用,同时考查了函数关系式的求法及方程的求法,同学们应该掌握.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 如图,小华和小丽两人玩游戏,她们准备了A、B两个分别被平均分成三个、四个扇形的转盘.游戏规则:小华转动A盘、小丽转动B盘.转动过程中,指针保持不动,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.两个转盘停止后指针所指区域内的数字之和小于6,小华获胜.指针所指区域内的数字之和大于6,小丽获胜.
如图,小华和小丽两人玩游戏,她们准备了A、B两个分别被平均分成三个、四个扇形的转盘.游戏规则:小华转动A盘、小丽转动B盘.转动过程中,指针保持不动,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.两个转盘停止后指针所指区域内的数字之和小于6,小华获胜.指针所指区域内的数字之和大于6,小丽获胜.
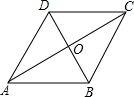 已知,如图在菱形ABCD中,对角线AC与BD相交于O,求证:AC平分∠BAD和∠BCD,BD平分∠ABC和∠ADC.
已知,如图在菱形ABCD中,对角线AC与BD相交于O,求证:AC平分∠BAD和∠BCD,BD平分∠ABC和∠ADC.