题目内容
8.已知⊙O的内接正六边形周长为12cm,则这个圆的半径是2cm.分析 首先求出∠AOB=$\frac{1}{6}$×360°,进而证明△OAB为等边三角形,问题即可解决.
解答 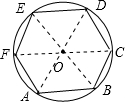 解:如图,
解:如图,
∵⊙O的内接正六边形ABCDEF的周长长为12cm,
∴边长为2cm,
∵∠AOB=$\frac{1}{6}$×360°=60°,且OA=OB,
∴△OAB为等边三角形,
∴OA=AB=2,
即该圆的半径为2,
故答案为:2.
点评 本题考查了正多边形和圆,以正多边形外接圆、正多边形的性质等几何知识点为考查的核心构造而成;灵活运用有关定理来分析、判断、推理或解答是关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
18.将抛物线y=x2向右平移2个单位,再向上平移3个单位后,抛物线的解析式为( )
| A. | y=(x+2)2+3 | B. | y=(x-2)2+3 | C. | y=(x+2)2-3 | D. | y=(x-2)2-3 |
19.桂林冬季里某一天最高气温是7℃,最低气温是-1℃,这一天桂林的温差是( )
| A. | -8℃ | B. | 6℃ | C. | 7℃ | D. | 8℃ |
3.下列一元二次方程中有两个不相等的实数根的方程是( )
| A. | (x-1)2=0 | B. | x2+2x-19=0 | C. | x2+4=0 | D. | x2+x+l=0 |
13.下列图案中,既是中心对称又是轴对称图形的个数有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 将△OAB绕着点O逆时针连续旋转两次得到△OA″B″,每次旋转的角度都是50°,若∠B″OA=120°,则∠AOB=20°°.
将△OAB绕着点O逆时针连续旋转两次得到△OA″B″,每次旋转的角度都是50°,若∠B″OA=120°,则∠AOB=20°°.