题目内容
 如图,⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM=3cm,则AB的长为( )
如图,⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM=3cm,则AB的长为( )| A、4cm | B、6cm |
| C、8cm | D、10cm |
考点:垂径定理,勾股定理
专题:
分析:连接OA,先根据⊙O的直径CD=10cm,AB⊥CD,可得出OA的长及AM=BM,再由勾股定理求出AM的长,进而可得出结论.
解答: 解:连接OA,
解:连接OA,
∵⊙O的直径CD=10cm,AB⊥CD,
∴OA=5cm,AM=BM,
∴AM=
=
=4(cm),
∴AB=2AM=8cm.
故选C.
 解:连接OA,
解:连接OA,∵⊙O的直径CD=10cm,AB⊥CD,
∴OA=5cm,AM=BM,
∴AM=
| OA2-OM2 |
| 52-32 |
∴AB=2AM=8cm.
故选C.
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
某三角形的三个内角之比为6:2:1,该三角形的形状是( )
| A、直角三角形 | B、锐角三角形 |
| C、钝角三角形 | D、无法确定 |
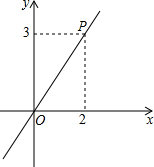 如图,已知正比例函数y=kx经过点P,
如图,已知正比例函数y=kx经过点P, ,怎么办呢?小明想了想,便翻看书后答案,此方程的解是x=-3,于是很快就补好了这个常数,他补出的这个常数是
,怎么办呢?小明想了想,便翻看书后答案,此方程的解是x=-3,于是很快就补好了这个常数,他补出的这个常数是 如图,将边长为a小正方形与边长为b的大正方形放在一起(b>a>0),用a、b表示△ABC的面积;
如图,将边长为a小正方形与边长为b的大正方形放在一起(b>a>0),用a、b表示△ABC的面积;