题目内容
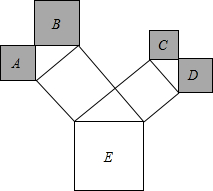如图，是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形E的面积是81，则图中所有正方形的面积和是（ ）| A、81 | B、162 |
| C、243 | D、324 |
考点：勾股定理
专题：
分析：根据正方形的面积公式，运用勾股定理可以证明：6个小正方形的面积和等于最大正方形面积的2倍．
解答：
解：根据勾股定理得到：A与B的面积的和是M的面积；C与D的面积的和是N的面积；而M，N的面积的和是E的面积．
即A、B、C、D、M、N的面积之和为2个E的面积．
∵正方形E的面积是81，
∴A、B、C、D、M、N、E的面积之和为81×3=243．
故选：C．
解：根据勾股定理得到：A与B的面积的和是M的面积；C与D的面积的和是N的面积；而M，N的面积的和是E的面积．即A、B、C、D、M、N的面积之和为2个E的面积．
∵正方形E的面积是81，
∴A、B、C、D、M、N、E的面积之和为81×3=243．
故选：C．
点评：考查了勾股定理，注意运用勾股定理和正方形的面积公式证明结论：6个小正方形的面积和等于最大正方形的面积的2倍．
练习册系列答案
相关题目
在下列立体图形中，它从正面看、从左面看、从上面看的图形能是如图的是（ ）| A、圆柱 | B、球 | C、圆锥 | D、三棱柱 |
若点P关于x轴的对称点的坐标是（2，3），则点P关于原点的对称点的坐标是（ ）
| A、（-3，-2） |
| B、（2，-3） |
| C、（-2，-3） |
| D、（-2，3） |
如图，已知AB∥DE，AB=DE，请你添加一个条件下列说法中正确的是（ ）
| A、三角形可分为斜三角形、直角三角形和锐角三角形 |
| B、等腰三角形任何一个内角都有可能是钝角或直角 |
| C、三角形外角一定是钝角 |
| D、在△ABC中，如果∠A=∠B=∠C，那么∠A=60°，∠C=60° |