题目内容
20. 如图,在△ABC中,AB=AC=10,BC=16,正方形DEFG的顶点D、G分别在AB、AC上,EF在BC上,求:正方形DEFG的边长.
如图,在△ABC中,AB=AC=10,BC=16,正方形DEFG的顶点D、G分别在AB、AC上,EF在BC上,求:正方形DEFG的边长.
分析 首先过点作AM⊥BC于点M,由AB=AC=10,BC=16,根据等腰三角形的性质与勾股定理,即可求得AM的长,又由四边形DEFG是矩形,易证得△ADG∽△ABC,设MN=DE=x,由相似三角形对应高的比等于相似比,即可得方程$\frac{DG}{16}$=$\frac{6-x}{6}$,则可表示出DG的长,由正方形的性质可得DE=DG,可得结果.
解答 解:过点作AM⊥BC于点M,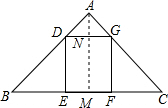 ∵AB=AC=10,BC=16,
∵AB=AC=10,BC=16,
∴BM=$\frac{1}{2}$BC=8,
在Rt△ABM中,AM=$\sqrt{{AB}^{2}{-BM}^{2}}$=6,
∵四边形DEFG是矩形,
∴DG∥EF,DE⊥BC,
∴AN⊥DG,四边形EDMN是矩形,
∴MN=DE,
设MN=DE=x,
∵DG∥EF,
∴△ADG∽△ABC,
∴DG:BC=AN:AM,
∴$\frac{DG}{16}$=$\frac{6-x}{6}$,
解得:DG=-$\frac{8}{3}$x+16,
∵四边形DEFG为正方形,
∴DE=DG,即x=-$\frac{8}{3}$x+16,
解得x=$\frac{48}{11}$,
∴正方形DEFG的边长为$\frac{48}{11}$.
点评 本题主要考查了相似三角形的判定与性质、矩形的性质以及勾股定理,注意辅助线的作法,注意掌握数形结合思想与方程思想的应用是解答此题的关键.

练习册系列答案
相关题目
11.下列图形是轴对称图形的是( )
| A. | 人的两点手 | B. | 两个1圆硬币 | C. | 线段 | D. | 平行四边形 |
15.把抛物线y=x2+4先向左平移1个单位,再向下平移3个单位,得到的抛物线的解析式为( )
| A. | y=(x+1)2+1 | B. | y=(x-1)2+1 | C. | y=(x-1)2+7 | D. | y=(x+1)2+7 |
5.点P关于x轴对称的点是(3,-4),则点P关于y轴对称的点的坐标在( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
12.实数-8的相反数是( )
| A. | 4 | B. | 8 | C. | -8 | D. | 0 |