题目内容
已知正实数a、b、c满足 =k,以2k,2k+1,2k-1为三边的三角形面积是
=k,以2k,2k+1,2k-1为三边的三角形面积是
- A.12
- B.6
- C.

- D.3
B
分析:本题通过对已知条件变形化简后得到a=b=c,可求得k的值,从而化简出以2k,2k+1,2k-1为三边的三角形的边长为3,4,5,进而根据直角三角形的面积公式求解.
解答:∵ ,
,
∴c(b+c)=a(a+b),b(a+b)=c(a+c),
化简后得:(c-a)(a+b+c)=0,(c-b)(a+b+c)=0,
∵a+b+c≠0,
∴a=b=c,
∴k=2,
∴以2k,2k+1,2k-1为三边分别为4,5,3;
∵32+42=52,
∴三角形为直角三角形,直角边的长分别为3,4,
根据直角三角形的面积公式,
∴S=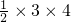 =6.
=6.
故选B.
点评:本题是一道通过对已知条件变形化简结合直角三角形的面积公式求解的综合题.通过审题把题目中的条件进行转化,是解题的关键.隐含了整体的数学思想和正确运算的能力.
分析:本题通过对已知条件变形化简后得到a=b=c,可求得k的值,从而化简出以2k,2k+1,2k-1为三边的三角形的边长为3,4,5,进而根据直角三角形的面积公式求解.
解答:∵
 ,
,∴c(b+c)=a(a+b),b(a+b)=c(a+c),
化简后得:(c-a)(a+b+c)=0,(c-b)(a+b+c)=0,
∵a+b+c≠0,
∴a=b=c,
∴k=2,
∴以2k,2k+1,2k-1为三边分别为4,5,3;
∵32+42=52,
∴三角形为直角三角形,直角边的长分别为3,4,
根据直角三角形的面积公式,
∴S=
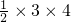 =6.
=6.故选B.
点评:本题是一道通过对已知条件变形化简结合直角三角形的面积公式求解的综合题.通过审题把题目中的条件进行转化,是解题的关键.隐含了整体的数学思想和正确运算的能力.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
已知正实数a、b、c满足
=
=
=k,以2k,2k+1,2k-1为三边的三角形面积是( )
| b+c |
| a |
| a+b |
| c |
| a+c |
| b |
| A、12 | ||
| B、6 | ||
C、
| ||
| D、3 |
已知正实数m的两个平方根为2x+3与y-4,且x-2y=3,则m为( )
| A、49 | B、25 | C、9 | D、1 |