题目内容
8. 在研究相似问题时,甲、乙同学的观点如下:
在研究相似问题时,甲、乙同学的观点如下:甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形相似.
对于两人的观点,下列说法正确的是( )
| A. | 甲对,乙不对 | B. | 甲不对,乙对 | C. | 两人都对 | D. | 两人都不对 |
分析 甲:根据题意得:AB∥A′B′,AC∥A′C′,BC∥B′C′,即可证得∠A=∠A′,∠B=∠B′,可得△ABC∽△A′B′C′;
乙:根据题意得:AB=CD=3,AD=BC=5,则A′B′=C′D′=3+2=5,A′D′=B′C′=5+2=7,则可得$\frac{AB}{A′B′}$≠$\frac{AD}{A′D′}$,即新矩形与原矩形不相似.
解答 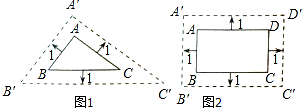 解:甲:根据题意得:AB∥A′B′,AC∥A′C′,BC∥B′C′,
解:甲:根据题意得:AB∥A′B′,AC∥A′C′,BC∥B′C′,
∴∠A=∠A′,∠B=∠B′,
∴△ABC∽△A′B′C′,
∴甲说法正确;
乙:∵根据题意得:AB=CD=3,AD=BC=5,则A′B′=C′D′=3+2=5,A′D′=B′C′=5+2=7,
∴$\frac{AB}{A′B′}$=$\frac{CD}{C′D′}$=$\frac{3}{5}$,$\frac{AD}{A′D′}$=$\frac{BC}{B′C′}$=$\frac{5}{7}$,
∴$\frac{AB}{A′B′}$≠$\frac{AD}{A′D′}$,
∴新矩形与原矩形不相似.
∴乙说法不正确.
故选:A.
点评 此题考查了相似三角形以及相似多边形的判定.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.某同学做了一道数学题:已知两个多项式A、B,计算2A+B,他误将“2A+B”看成“A+2B”,求得的结果是9x2-2x+7,已知B=x2+3x-2,则2A+B的正确答案为15x2-13x+20.
20.下列各数:-$\frac{4}{5}$,1,8.6,-7,0,$\frac{5}{6}$,-4$\frac{2}{3}$,+101,-0.05,-9中( )
| A. | 只有1,-7,+101,-9是整数 | B. | 其中有三个数是正整数 | ||
| C. | 非负数有1,8.6,0,$\frac{5}{6}$,+101 | D. | 只有-$\frac{4}{5}$,-4$\frac{2}{3}$是负分数 |
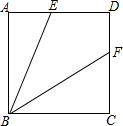 已知:如图,在正方形ABCD中,E为AD上一点,BF平分∠CBE交CD于F,若正方形边长为2$\sqrt{5}$,AE=4,求DF的长.
已知:如图,在正方形ABCD中,E为AD上一点,BF平分∠CBE交CD于F,若正方形边长为2$\sqrt{5}$,AE=4,求DF的长. △ABC中,AB=4,AC=3,∠C-∠B=90°,求BC的长.
△ABC中,AB=4,AC=3,∠C-∠B=90°,求BC的长.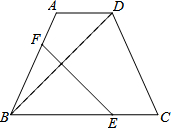 如图,在等腰梯形ABCD中,AD∥BC,∠ADB=45°,翻折梯形ABCD,使点B与点D重合,折痕分别交边AB、BC于点F、E,若AD=6,BC=14,那么cot∠C=$\frac{2}{5}$.
如图,在等腰梯形ABCD中,AD∥BC,∠ADB=45°,翻折梯形ABCD,使点B与点D重合,折痕分别交边AB、BC于点F、E,若AD=6,BC=14,那么cot∠C=$\frac{2}{5}$.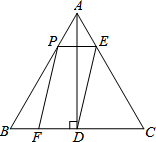 如图,在等边三角形ABC中,AB=6,AD⊥BC于点D,点P在边AB上运动,过点P作PE∥BC与边AC交于点E,连接ED,以PE,ED为邻边作?PEDF,设?PEDF与△ABC重叠部分图形的面积为y,线段AP的长为x(0<x<6).
如图,在等边三角形ABC中,AB=6,AD⊥BC于点D,点P在边AB上运动,过点P作PE∥BC与边AC交于点E,连接ED,以PE,ED为邻边作?PEDF,设?PEDF与△ABC重叠部分图形的面积为y,线段AP的长为x(0<x<6).