题目内容
17.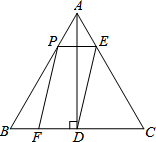 如图,在等边三角形ABC中,AB=6,AD⊥BC于点D,点P在边AB上运动,过点P作PE∥BC与边AC交于点E,连接ED,以PE,ED为邻边作?PEDF,设?PEDF与△ABC重叠部分图形的面积为y,线段AP的长为x(0<x<6).
如图,在等边三角形ABC中,AB=6,AD⊥BC于点D,点P在边AB上运动,过点P作PE∥BC与边AC交于点E,连接ED,以PE,ED为邻边作?PEDF,设?PEDF与△ABC重叠部分图形的面积为y,线段AP的长为x(0<x<6).(1)求线段PE的长(用含x的代数式表示);
(2)当四边形PEDF为菱形时,求x的值;
(3)求y与x之间的函数关系式.
分析 (1)由PE与BC平行,得到三角形APE与三角形ABC相似,根据三角形ABC为等边三角形,得到三角形APE为等边三角形,可得出PE=AP=x;
(2)若四边形PEDF为菱形,得到PE=DE=x,由三角形APE为等边三角形得到AE=PE,可得出AE=DE,利用等边对等角得到∠DAC=∠ADE,利用等式的性质得到∠EDC=∠C,利用等角对等边得到DE=EC,即可求出x的值;
(3)分两种情况考虑:当0<x≤3时,重合部分就是平行四边形PEDF,如图1;当3<x<6时,重合部分是梯形PEDB,如图2,分别求出y与x的函数关系式即可.
解答 解:(1)∵PE∥BC,
∴△APE∽△ABC,
∵△ABC为等边三角形,
∴△APE为等边三角形,
∴PE=AP=x(0<x<6);
(2)∵四边形PEDF为菱形,
∴PE=DE=x,
∵△APE为等边三角形,即AE=PE,
∴AE=DE,
∴∠DAC=∠ADE,
∵∠ADE+∠EDC=∠DAC+∠C=90°,
∴∠EDC=∠C,
∴DE=EC,
∴DE=EC=AE=$\frac{1}{2}$AC=$\frac{1}{2}$AB=3,
则x=3;
(3)当x=3,即P为AB的中点时,PE=$\frac{1}{2}$BC,则F与B重合,
当0<x≤3时,重合部分就是平行四边形PEDF,如图1,
在等边△ABC中,AD=AB•sin60°=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
在等边△APE中,AM=AP•sin60°=$\frac{\sqrt{3}}{2}$x,则DM=3$\sqrt{3}$-$\frac{\sqrt{3}}{2}$x,
此时y=x(3$\sqrt{3}$-$\frac{\sqrt{3}}{2}$x)=-$\frac{\sqrt{3}}{2}$x2+3$\sqrt{3}$x;
当3<x<6时,重合部分是梯形PEDB,如图2,
此时y=$\frac{1}{2}$(PE+FD)•DM=$\frac{1}{2}$×(x+3)×(3$\sqrt{3}$-$\frac{\sqrt{3}}{2}$x)=-$\frac{\sqrt{3}}{4}$x2+$\frac{3\sqrt{3}}{4}$x+$\frac{9\sqrt{3}}{2}$.
点评 此题属于相似形综合题,涉及的知识有:相似三角形的判定与性质,等边三角形的判定与性质,菱形的性质,平行的性质,以及平行四边形的面积,熟练掌握相似三角形的判定与性质是解本题的关键.

 在研究相似问题时,甲、乙同学的观点如下:
在研究相似问题时,甲、乙同学的观点如下:甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形相似.
对于两人的观点,下列说法正确的是( )
| A. | 甲对,乙不对 | B. | 甲不对,乙对 | C. | 两人都对 | D. | 两人都不对 |
| A. | 75° | B. | 105° | C. | 90° | D. | 60° |
 在△ABC中,如图所示,AD=AE,DB=EC,P为CD、BE的交点,则图中全等三角形的对数是( )
在△ABC中,如图所示,AD=AE,DB=EC,P为CD、BE的交点,则图中全等三角形的对数是( )| A. | 3对 | B. | 4对 | C. | 5对 | D. | 6对 |
| A. | 角平分线 | B. | 高 | C. | 中线 | D. | 垂直平分线 |
 如图,在△ABC中,∠ACB=90°,CD⊥AB,D为垂足,AC=6cm,BC=8cm.
如图,在△ABC中,∠ACB=90°,CD⊥AB,D为垂足,AC=6cm,BC=8cm. 已知:如图,点A、B、C、D在同一条直线上,AE∥BF,AE=BF,AB=CD.求证:(1)CE=DF,
已知:如图,点A、B、C、D在同一条直线上,AE∥BF,AE=BF,AB=CD.求证:(1)CE=DF,