Question

13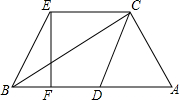．如图，在Rt△ABC中，∠ACB=90°，点D是AB上的一点，连接CD，CE∥AB，BE∥CD，且CE=AD．
（1）求证：四边形BDCE是菱形；
（2）过点E作EF⊥BD，垂足为点F，若点F是BD的中点，EB=6，求BC的长．

Answer 1

分析 （1）先证明四边形BDCE是平行四边形，得出CE=BD，证出BD=CD，由直角三角形斜边上的中线性质得出CD=$\frac{1}{2}$AB=BD，即可得出四边形BDCE是菱形；
（2）连接DE，由菱形的性质得出BC⊥DE，BD=BE，OB=OC，由线段垂直平分线的性质得出BE=DE，证出BE=DE=BD，由等边三角形和菱形的性质得出∠EBC=$\frac{1}{2}$∠EBD=30°，求出OE=$\frac{1}{2}$EB=3，由勾股定理求出OB，即可得出结果．

解答 （1）证明：∵CE∥AB，BE∥CD，
∴四边形BDCE是平行四边形，
∴CE=BD，
∵CE=AD，
∴BD=CD，
又∵∠ACB=90°，
∴CD=$\frac{1}{2}$AB=BD，
∴四边形BDCE是菱形；
（2）解：连接DE，如图所示：
由（1）得：四边形BDCE是菱形，
∴BC⊥DE，BD=BE，OB=OC，
∵EF⊥BD，点F是BD的中点，
∴BE=DE，
∴BE=DE=BD，
∴∠DBE=60°，∠EBC=$\frac{1}{2}$∠EBD=30°，
∴OE=$\frac{1}{2}$EB=3，
∴OB=$\sqrt{E{B}^{2}-O{E}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$，
∴BC=2OB=6$\sqrt{3}$．

点评 本题考查了平行四边形的判定与性质、菱形的判定与性质、等边三角形的性质、直角三角形斜边上的中线性质、勾股定理等知识；熟练掌握菱形的判定与性质是解决问题的关键．