题目内容
(1)如图①,若BC=6,AC=4,∠C=60°,求△ABC的面积S△ABC ;
(2)如图②,若BC=a,AC=b,∠C=α,求△ABC的面积S△ABC ;
(3)如图③,四边形ABCD,若AC=m,BD=n,对角线AC、BD交于O点,它们所成
的锐角为β.求四边形ABCD的面积S四边形ABCD .
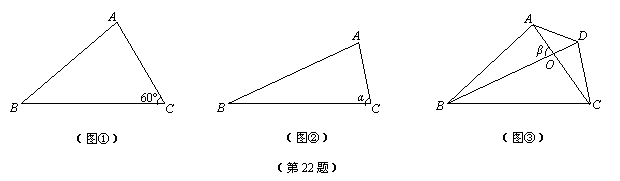
(1)如图①,过点A作AH⊥BC,垂足为H.
在Rt△AHC 中,
中,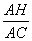 =sin60°,
=sin60°,
∴AH=AC·sin60°=4×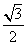 =2
=2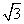 .
.
∴S△ABC= ×BC×AH=
×BC×AH= ×6×2
×6×2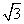 =6
=6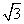 .
.
(2)如图②,过点A作AH⊥BC,垂足为H.
在Rt△AHC中,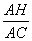 =sinα,
=sinα,
∴AH=AC·sinα=b sinα.
∴S△ABC= ×BC×AH=
×BC×AH= ab sinα
ab sinα
(3)如图③,分别过点A,C作AH⊥BD,CG⊥BD,垂足为H,G.
在Rt△AHO与Rt△CGO中,AH=OAsinβ,CG=OCsinβ;
于是,S△ABD= ×BD×AH=
×BD×AH= n×OAsinβ;
n×OAsinβ;
S△BCD= ×BD×CG=
×BD×CG= n×OCsinβ;
n×OCsinβ;
∴S四边形ABCD= S△ABD+S△BCD= n×OAsinβ+
n×OAsinβ+ n×OCsinβ=
n×OCsinβ= n×(OA+OC)sinβ
n×(OA+OC)sinβ
 =
= mnsinβ.
mnsinβ.

练习册系列答案
相关题目
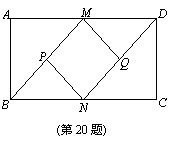
如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(0,4)、(-3,0),点E、F分别为AB、BO的中点,分别连接AF、EO,交点为P,点P坐标为
| A.(- | B.(- | C.(-1, | D.(-1,2) |
 |
 ,
, )
)
 -
- .
. (k为常数,k≠0)的图象是双曲线.当k>0时,双曲线两个分支分别在
(k为常数,k≠0)的图象是双曲线.当k>0时,双曲线两个分支分别在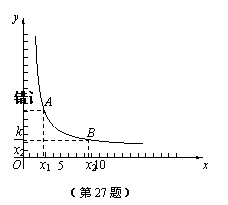 这些我们熟悉的性质,可以通过说理得到吗?
这些我们熟悉的性质,可以通过说理得到吗? ),B(x2,
),B(x2, ),
),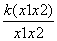 .
. (2)分别写出二次函数y=ax2 (a>0,a为常数)的对称性和增减性,并进行说理.
(2)分别写出二次函数y=ax2 (a>0,a为常数)的对称性和增减性,并进行说理. 时函数取得最小值.
时函数取得最小值.  ,
, ,则
,则 的度数
的度数 B.
B. C.
C. D.
D.

 .
.
