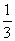题目内容
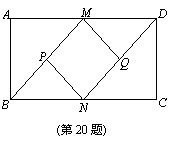
如图,在矩形ABCD中,M、N分别AD、BC的中点,P、Q分别BM、DN
的中点.
(1)求证:四边形MPNQ是菱形;
(2)若AB=2,BC=4,求四边形MPNQ的面积.
 |
(1)证明:∵四边形ABCD是矩形,
∴AD=BC,AD∥BC.
连结MN,∵M、N分别AD、BC的中点,
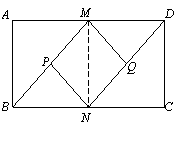 ∴MD=
∴MD=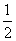 AD,BN=
AD,BN=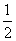 BC.
BC.
∴MD=BN,MD∥ BN,∴四边形BNDM是平行四边形.
BN,∴四边形BNDM是平行四边形.
∴MB=ND.
∵P、Q分别BM、DN的中点,∴MP=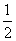 MB,NQ=
MB,NQ=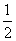 DN.
DN.
∴MP=NQ.
又∵MP∥NQ,∴四边形MPNQ是平 行四边形.
行四边形.
 ∵ABCD为矩形,M、N分别AD、BC的中点,
∵ABCD为矩形,M、N分别AD、BC的中点,
∴四边形ABNM为矩形,∴MN⊥BC.
∴在Rt△MNB中,PN=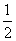 BM.∴PN=PM.
BM.∴PN=PM.
∴四边形MPNQ是菱形.
(2)∵AB=2,BC=4,∴MN=BN=2
∵P为MB的中点,∴PN⊥MB,PN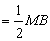
在Rt△MNB中,MB=
∴ ,∴四边形MPNQ是边长为
,∴四边形MPNQ是边长为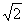 的正方形.
的正方形.
∴四边形MPNQ的面积为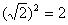

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
正n边形的每个内角都是140°,则n为
| A.7 | B.8 | C.9 | D.10 |
反比例函数y= 和正比例函数y=mx的部分图象如图所示.
和正比例函数y=mx的部分图象如图所示.
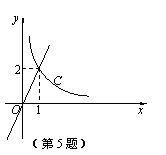 由此可以得到方程
由此可以得到方程 =mx的实数根为
=mx的实数根为
| A.x=1 | B.x=2 |
| C.x1=1,x2=-1 | D.x1=1,x2=-2 |
 其中x满足方程x2+4x-5=0.
其中x满足方程x2+4x-5=0. ·
· 的结果是 .
的结果是 . 是半圆,O为AB中点,C、D两点在
是半圆,O为AB中点,C、D两点在 =62°,则∠ABD的度数为 .
=62°,则∠ABD的度数为 .

 这时小明在剩下的啤酒中任
这时小明在剩下的啤酒中任 B.
B. C.
C.  D.
D.