题目内容
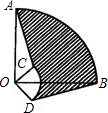 如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,OA=3,OC=1,分别连接AC、BD,则图中阴影部分的面积为( )
如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,OA=3,OC=1,分别连接AC、BD,则图中阴影部分的面积为( )A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |
分析:通过分析图可知:△ODB经过旋转90°后能够和△OCA重合(证全等也可),因此图中阴影部分的面积=扇形AOB的面积-扇形COD的面积,所以S阴=
π×(9-1)=2π.
| 1 |
| 4 |
解答:解:由图可知,将△OAC顺时针旋转90°后可与△ODB重合,
∴S△OAC=S△OBD;
因此S阴影=S扇形OAB+S△OBD-S△OAC-S扇形OCD=S扇形OAB-S扇形OCD=
π×(9-1)=2π.
故选C.
∴S△OAC=S△OBD;
因此S阴影=S扇形OAB+S△OBD-S△OAC-S扇形OCD=S扇形OAB-S扇形OCD=
| 1 |
| 4 |
故选C.
点评:本题中阴影部分的面积可以看作是扇形AOB与扇形COD的面积差,求不规则的图形的面积,可以转化为几个规则图形的面积的和或差来求.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
 如图,圆心角都是90°的扇形OAB与扇形OCD如图那样叠放在一起,连接AC、BD.求证:△AOC≌△BOD.
如图,圆心角都是90°的扇形OAB与扇形OCD如图那样叠放在一起,连接AC、BD.求证:△AOC≌△BOD. 如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,OA=3,OC=1,分别连接AC、BD,则图中阴影部分的面积为
如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,OA=3,OC=1,分别连接AC、BD,则图中阴影部分的面积为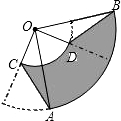
 如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连接AC,BD.
如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连接AC,BD.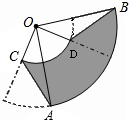 如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连接AC、BD.
如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连接AC、BD.