题目内容
如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连接AC,BD.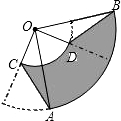
(1)求证:AC=BD;
(2)若图中阴影部分的面积是
| 3 | 4 |
分析:(1)求证:AC=BD,则需求证△AOC≌△BOD,利用已知条件证明即可.
(2)从图中可以得S阴影就是大扇形减小扇形形所得的弓形的面积,根据扇形的面积公式计算即可.
(2)从图中可以得S阴影就是大扇形减小扇形形所得的弓形的面积,根据扇形的面积公式计算即可.
解答:(1)证明:∵∠AOB=∠COD=90°,
∴∠AOC+∠AOD=∠BOD+∠AOD;
∴∠AOC=∠BOD;
在△AOC和△BOD中,
∵
,
∴△AOC≌△BOD(SAS);
∴AC=BD.
(2)解:根据题意得:S阴影=
-
=
;
∴
π=
;
解得:OC=1(cm).
∴∠AOC+∠AOD=∠BOD+∠AOD;
∴∠AOC=∠BOD;
在△AOC和△BOD中,
∵
|
∴△AOC≌△BOD(SAS);
∴AC=BD.
(2)解:根据题意得:S阴影=
| 90π•OA2 |
| 360 |
| 90π•OC2 |
| 360 |
| 90π•(OA2-OC2) |
| 360 |
∴
| 3 |
| 4 |
| 90π(22-OC2) |
| 360 |
解得:OC=1(cm).
点评:本题考查了全等三角形的判定和性质、扇形面积的计算方法等知识点.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 如图,圆心角都是90°的扇形OAB与扇形OCD如图那样叠放在一起,连接AC、BD.求证:△AOC≌△BOD.
如图,圆心角都是90°的扇形OAB与扇形OCD如图那样叠放在一起,连接AC、BD.求证:△AOC≌△BOD. 如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,OA=3,OC=1,分别连接AC、BD,则图中阴影部分的面积为
如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,OA=3,OC=1,分别连接AC、BD,则图中阴影部分的面积为 如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连接AC,BD.
如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连接AC,BD.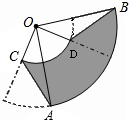 如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连接AC、BD.
如图,圆心角都是90°的扇形OAB与扇形OCD叠放在一起,连接AC、BD.