题目内容
2．两个相似多边形的面积比是4：25，则它们周长比是2：5．分析 由两个相似多边形的面积比是4：25，根据相似多边形的面积比等于相似比的平方，即可求得其相似比，又由相似多边形的周长的比等于相似比，求得答案．
解答 解：∵两个相似多边形的面积比是4：25，
∴它们的相似比为：2：5，
∴它们周长比是：2：5．
故答案为：2：5．
点评 此题考查了相似多边形的性质．注意熟记定理是解此题的关键．
练习册系列答案
相关题目
14．两年前生产某药品的成本是5000元，现在生产这种药品的成本是3000元，设该药品成本的年平均下降率为x，则下面所列方程中正确的是（ ）
| A． | 5000（1-2x）=3000 | B． | 3000（1+2x）=5000 | C． | 3000（1+x）2=5000 | D． | 5000（1-x）2=3000 |
11．
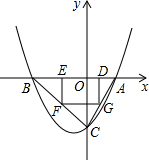如图，已知抛物线P：y=ax2+bx+c（a≠0）与x轴交于A、B两点（点A在x轴的正半轴上），与y轴交于点C，矩形DEFG的一条边DE在线段AB上，顶点F、G分别在线段BC、AC上，抛物线P上部分点的横坐标对应的纵坐标如下：
（1）求抛物线表达式及A、B、C三点的坐标；
（2）若点D的坐标为（m，0），矩形DEFG的面积为S，求S与m的函数关系，并求出面积的最大值及m的取值范围．
如图，已知抛物线P：y=ax2+bx+c（a≠0）与x轴交于A、B两点（点A在x轴的正半轴上），与y轴交于点C，矩形DEFG的一条边DE在线段AB上，顶点F、G分别在线段BC、AC上，抛物线P上部分点的横坐标对应的纵坐标如下：| x | … | -3 | -2 | 1 | 2 | … |
| y | … | $-\frac{5}{2}$ | -4 | $-\frac{5}{2}$ | 0 | … |
（2）若点D的坐标为（m，0），矩形DEFG的面积为S，求S与m的函数关系，并求出面积的最大值及m的取值范围．
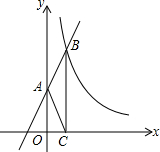如图，直线y=2x+2与y轴交于A点，与反比例函数y=$\frac{k}{x}$（x＞0）的图象交于点B，过点B作BC⊥x轴于点C，连接AC，若tan∠ACO=2，则此反比例函数解析式为y=$\frac{4}{x}$．