题目内容
15.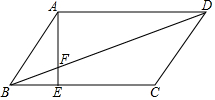 如图,点E是平行四边形ABCD的边BC上的三等分点,连接AE交对角线BD于点F,若△ADF的面积为18cm2,则S△ABF的面积是6cm2.
如图,点E是平行四边形ABCD的边BC上的三等分点,连接AE交对角线BD于点F,若△ADF的面积为18cm2,则S△ABF的面积是6cm2.
分析 由平行四边形的性质得出AD∥BC,AD=BC=3BE,证出△ADF∽△EBF,得出DF:BF=AD:BE=3:1,$\frac{{S}_{△ADF}}{{S}_{△ABF}}$=3,即可得出结果.
解答 解:∵点E是平行四边形ABCD的边BC上的三等分点,
∴BC=3BE,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=3BE,
∴△ADF∽△EBF,
∴DF:BF=AD:BE=3:1,
∴$\frac{{S}_{△ADF}}{{S}_{△ABF}}$=3,
∴S△ABF=$\frac{1}{3}$×18=6(cm2);
故答案为:6cm2.
点评 本题考查相似三角形的判定和性质、平行四边形的性质等知识,解题的关键是熟练掌握相似三角形的判定和性质,属于中考常考题型.

练习册系列答案
相关题目
6.(1)图(1)是正方体木块,把它切去一块,可能得到形如图(2),(3),(4),(5)的木块.

我们知道,图(1)的正方体木块有8个顶点,12条棱,6个面,请你将图(2),(3),(4),(5)中木块的顶点数,棱数,面数填入表:
(2)观察表,请你归纳上述各种木块的顶点数,棱数,面数之间的数量关系,这种数量关系是:
顶点数+面数-2=棱数.
(3)图⑥是用虚线画出的正方体木块,请你想象一种与图②~⑤不同的切法,把切去一块后得到的那一块的每条棱都改画成实线,则该木块的顶点数为8,棱数为12,面数为6.这与你(2)题中所归纳的关系是否相符?


我们知道,图(1)的正方体木块有8个顶点,12条棱,6个面,请你将图(2),(3),(4),(5)中木块的顶点数,棱数,面数填入表:
| 图 | 顶点数 | 棱数 | 面数 |
| (1) | 8 | 12 | 6 |
| (2) | 6 | 9 | 5 |
| (3) | 8 | 12 | 6 |
| (4) | 8 | 13 | 7 |
| (5) | 10 | 15 | 7 |
顶点数+面数-2=棱数.
(3)图⑥是用虚线画出的正方体木块,请你想象一种与图②~⑤不同的切法,把切去一块后得到的那一块的每条棱都改画成实线,则该木块的顶点数为8,棱数为12,面数为6.这与你(2)题中所归纳的关系是否相符?

3.下列图形中不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4.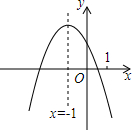 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc<0;②a+b+c<0;③4a+c>2b;④2a-b=0;⑤m(am+b)+b<a(m≠-1),其中,正确的结论有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc<0;②a+b+c<0;③4a+c>2b;④2a-b=0;⑤m(am+b)+b<a(m≠-1),其中,正确的结论有( )
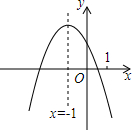 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc<0;②a+b+c<0;③4a+c>2b;④2a-b=0;⑤m(am+b)+b<a(m≠-1),其中,正确的结论有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下四个结论:①abc<0;②a+b+c<0;③4a+c>2b;④2a-b=0;⑤m(am+b)+b<a(m≠-1),其中,正确的结论有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
5.人类遗传物质DNA是一个很长的链,最短的22号染色体也长达30 000 000个核苷酸.数据30 000 000用科学记数法表示为( )
| A. | 3×107 | B. | 30×106 | C. | 0.3×108 | D. | 3×108 |
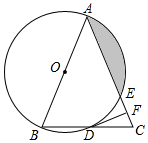 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC;垂足为点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作DF⊥AC;垂足为点F. 如图,P为矩形ABCD边上的一个动点,沿ABCD方向运动,P点运动的路程为x.△PAD的面积为y,则y与x的函数关系用图象表示大致是( )
如图,P为矩形ABCD边上的一个动点,沿ABCD方向运动,P点运动的路程为x.△PAD的面积为y,则y与x的函数关系用图象表示大致是( )


