题目内容
 如图,在△ABC中,AD、BE是中线,AD、BE交于点P,已知△ABC的面积为4,求四边形DCEP的面积
如图,在△ABC中,AD、BE是中线,AD、BE交于点P,已知△ABC的面积为4,求四边形DCEP的面积考点:三角形的重心,三角形的面积
专题:
分析:如图,作辅助线,运用重心的性质分别求出△DPC、△EPC的面积,即可解决问题.
解答: 解:如图,连接PC;
解:如图,连接PC;
设△ABC、△ADC、△APC、△DPC,
△PEC的面积分别为α、β、γ、θ、λ;
∵AD、BE是中线,
∴BD=CD、AE=CE、AP=2PD;
∴β=
α=
×4=2;θ=
β=
,γ=
β=
,
S△PEC=
γ=
,
∴四边形DCEP的面积=
+
=
.
故答案为
.
 解:如图,连接PC;
解:如图,连接PC;设△ABC、△ADC、△APC、△DPC,
△PEC的面积分别为α、β、γ、θ、λ;
∵AD、BE是中线,
∴BD=CD、AE=CE、AP=2PD;
∴β=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
S△PEC=
| 1 |
| 2 |
| 2 |
| 3 |
∴四边形DCEP的面积=
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
故答案为
| 4 |
| 3 |
点评:该题主要考查了三角形重心的性质及其应用问题;解题的关键是作辅助线,灵活运用重心的性质等几何知识点来解题.

练习册系列答案
相关题目
 如图是由几个相同的正方体搭成的一个几何体,从正面看到的平面图形是( )
如图是由几个相同的正方体搭成的一个几何体,从正面看到的平面图形是( )A、 |
B、 |
C、 |
D、 |
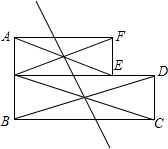 如图是由两个矩形组成的组合图形,能否在图形中找到一点P,沿过点P的某一条直线折叠该图形,能将该图形分成面积相等的两部分?若能,请你在图中做出点P,并说明点P的位置;若不能,请说明理由.
如图是由两个矩形组成的组合图形,能否在图形中找到一点P,沿过点P的某一条直线折叠该图形,能将该图形分成面积相等的两部分?若能,请你在图中做出点P,并说明点P的位置;若不能,请说明理由.
 如图,直线AB与CD相交于点O,OE平分∠AOD,OF平分∠BOD.
如图,直线AB与CD相交于点O,OE平分∠AOD,OF平分∠BOD.