题目内容
如图，△ABC中，AB=18，AC=16，D在AB上，AD=9，在AC上取一点P，问AP=考点：相似三角形的判定
专题：
分析：因为AB和AC、AD和AP有共同的夹角∠A，故使得
=
或
=
，即可求出AP的长度，即可解题．
| AB |
| AC |
| AP |
| AD |
| AB |
| AC |
| AD |
| AP |
解答：解：∵AB和AC、AD和AP有共同的夹角∠A，
∴
=
或
=
，均可使得△ADP和△ABC相似，
∴
=
或
=
解得AP=
或8．
故答案为：8或
．
∴
| AB |
| AC |
| AP |
| AD |
| AB |
| AC |
| AD |
| AP |
∴
| 18 |
| 16 |
| AP |
| 9 |
| 18 |
| 16 |
| 9 |
| AP |
解得AP=
| 81 |
| 9 |
故答案为：8或
| 81 |
| 8 |
点评：本题考查了相似三角形对应边比值相等的性质，本题中讨论
=
或
=
是解题关键．
| AB |
| AC |
| AP |
| AD |
| AB |
| AC |
| AD |
| AP |
练习册系列答案
相关题目
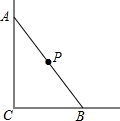如图所示，一根长为5米的木棍AB，斜靠在与地面垂直的墙上．设木棍的中点为P，若棍子A端沿墙下滑，且B端沿地面向右滑行．请判断木棍滑动的过程中，点P到点C的距离是否发生变化：
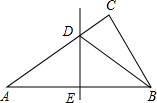如图，在△ABC中，∠C=90°，DE垂直平分AB，交AC于点D，交AB于点E，若∠A=35°．求∠CBD的度数．