题目内容
 如图一次函数y=-
如图一次函数y=-
| ||
| 3 |
(1)求△ABC的面积;
(2)在x轴上,是否存在点M,使△MAB为等腰三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
分析:(1)由一次函数解析式可求出OA、OB的长度,在Rt△OAB中可求出AB的长度,再由等边三角形的性质可求出△ABC的面积;
(2)①以AB为腰的等腰三角形有三个,②以AB为底边的等腰三角形有1一个,分别求出点M的坐标即可.
(2)①以AB为腰的等腰三角形有三个,②以AB为底边的等腰三角形有1一个,分别求出点M的坐标即可.
解答:解:(1)∵函数解析式为:y=-
x+1,
∴点B坐标为(0,1),点A坐标为(
,0),
∴OA=
,OB=1,
在Rt△OAB中,AB=
=2,
则等边三角形ABC的面积为
AB2=
.
(2)存在点M,使△MAB为等腰三角形
①若以AB为腰,如图所示:

当点M位于M1位置时,OM1=OA+AM1=OA+AB=2+
,
此时点M1坐标为(2+
,0);
当点M位于M2位置时,OM2=OA=
,
此时点M2坐标为(-
,0);
当点M位于M3位置时,OM3=AB=2,
此时点M3坐标为(
-2,0);
②若以AB为底边,如图所示:

作AB的中垂线交x轴于点M4,则此时△M4AB为等腰三角形,
∵OB=1,OA=
,
∴∠OAB=30°,
∵AB=2,M4N是AB的中垂线,
∴AN=1,
在Rt△ANM4中,AM4=
=
,
则OM4=OA-AM4=
,
则此时M4的坐标为(
,0).
综上可得存在点M,使△MAB为等腰三角形,点M的坐标为:M1(2+
,0)或M2(-
,0)或M3(
-2,0)或M4(
,0).
| ||
| 3 |
∴点B坐标为(0,1),点A坐标为(
| 3 |
∴OA=
| 3 |
在Rt△OAB中,AB=
| OB2+OA2 |
则等边三角形ABC的面积为
| ||
| 4 |
| 3 |
(2)存在点M,使△MAB为等腰三角形
①若以AB为腰,如图所示:

当点M位于M1位置时,OM1=OA+AM1=OA+AB=2+
| 3 |
此时点M1坐标为(2+
| 3 |
当点M位于M2位置时,OM2=OA=
| 3 |
此时点M2坐标为(-
| 3 |
当点M位于M3位置时,OM3=AB=2,
此时点M3坐标为(
| 3 |
②若以AB为底边,如图所示:

作AB的中垂线交x轴于点M4,则此时△M4AB为等腰三角形,
∵OB=1,OA=
| 3 |
∴∠OAB=30°,
∵AB=2,M4N是AB的中垂线,
∴AN=1,
在Rt△ANM4中,AM4=
| AN |
| cos∠OAB |
2
| ||
| 3 |
则OM4=OA-AM4=
| ||
| 3 |
则此时M4的坐标为(
| ||
| 3 |
综上可得存在点M,使△MAB为等腰三角形,点M的坐标为:M1(2+
| 3 |
| 3 |
| 3 |
| ||
| 3 |
点评:本题考查了一次函数综合题,涉及了点的坐标与线段长度之间的转换,含30°角的直角三角形的性质及等边三角形的性质,解答本题需要我们数形结合,将所学的知识点串在一起,融会贯通,灵活求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图一次函数y=kx+b的图象与反比例函数
如图一次函数y=kx+b的图象与反比例函数 图象在第二象限交于点C(m,6),CD⊥x轴于点D,OA=OD.
图象在第二象限交于点C(m,6),CD⊥x轴于点D,OA=OD.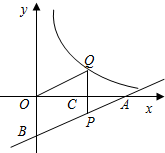 (2012•市中区一模)如图一次函数
(2012•市中区一模)如图一次函数 (2013•湖州一模)如图一次函数y=kx+b的图象经过点A(-1,3)和点B(2,-3).
(2013•湖州一模)如图一次函数y=kx+b的图象经过点A(-1,3)和点B(2,-3).