Question

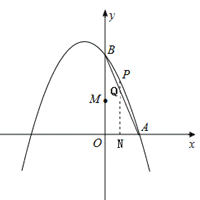
【题目】如图，已知抛物线经过A（1，0），B（0，3）两点，对称轴是直线x=﹣1．

（1）求抛物线对应的函数关系式；

（2）点N在线段OA上，点M在线段OB上，且OM=2ON，过点N作x轴的垂线交线段AB于点Q，交抛物线于点P．

①当ON为何值时，四边形OMPN为矩形；

②△AOQ能否为等腰三角形？若能，求出此时ON的值；若不能，请说明理由．

Answer 1

【答案】（1）抛物线的解析式为；（2）①，②或或1﹣.

【解析】试题分析：（1）可设顶点式，根据待定系数法可求抛物线对应的函数关系式；

（2）①当四边形OMPN为矩形时，满足条件OM=PN，据此列一元二次方程求解；

②△AOQ为等腰三角形时，可能存在三种情形，需要分类讨论，逐一计算．

试题解析：解：（1）根据题意，设抛物线的解析式为：y=a（x+1）2+k．∵点A（1，0），B（0，3）在抛物线上，∴，解得： ，∴抛物线的解析式为：y=﹣（x+1）2+4；

（2）①设ON=t（0＜t＜1）．则OM=2t，PN=﹣（t+1）2+4．∵四边形OMPN为矩形，∴OM=PN，即2t=﹣（t+1）2+4，整理得：t2+4t﹣3=0，解得t=﹣2，由于t=﹣﹣2＜0，故舍去，∴当ON=﹣2时，四边形OMPN为矩形；

②Rt△AOB中，OA=1，OB=3，∴tanA=3．

若△AOQ为等腰三角形，有三种情况：

（I）若OQ=AQ，如答图1所示：

则N为OA中点，ON=OA=，∴ON=；

（II）若OQ=OA，如答图2所示：

设AN=x，则QD=ADtanA=3x，ON=OA﹣AN=1﹣x．在Rt△QON中，由勾股定理得：ON2+QN2=OQ2，即（1﹣x）2+（3x）2=12，解得x1=，x2=0（舍去），∴x=，ON=1﹣x=，∴ON=；

（III）若OA=AQ，如答图3所示：

设AN=x，则QD=ANtanA=3x．在Rt△AQN中，由勾股定理得：QN2+AN2=AQ2，即x2+（3x）2=12，解得x1=，x2=﹣（舍去），∴ON=1﹣x=1﹣，∴ON=1﹣．

综上所述：当ON为、、（1﹣）时，△AOQ为等腰三角形．