题目内容
12．
如图是两个可以自由转动的转盘，转盘A被分成三个面积相等的扇形，转盘B被分成两个面积相等的扇形．（1）转动转盘A一次，所得到的数字是负数的概率为$\frac{1}{3}$；
（2）转动两个转盘各一次，请用列表法或画树状图法求所得到的数字均是负数的概率．
分析 （1）由转盘A被分成三个面积相等的扇形，是负数的只有1种情况，直接利用概率公式求解即可求得答案；
（2）首先根据题意列出表格，然后由树状图求得所有等可能的结果与所得到的数字均是负数的情况，再利用概率公式即可求得答案．
解答 解：（1）∵转盘A被分成三个面积相等的扇形，是负数的只有1种情况，
∴转动转盘A一次，所得到的数字是负数的概率为：$\frac{1}{3}$；
故答案为：$\frac{1}{3}$；
（2）列表得：
| 1 | -1 | 0 | |
| 2 | （1，2） | （-1，2） | （0，2） |
| -2 | （1，-2） | （-1，-2） | （0，-2） |
∴P（得到数字均是负数）=$\frac{1}{6}$．
点评 此题考查了列表法或树状图法求概率．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
3．
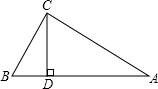如图，已知Rt△ABC中，∠ACB=90°，CD是高，∠A=30°，BD=2cm，求AB的长（ ）
如图，已知Rt△ABC中，∠ACB=90°，CD是高，∠A=30°，BD=2cm，求AB的长（ ）| A． | 4 | B． | 6 | C． | 8 | D． | 10 |
如图，用长为24m的篱笆，一面利用墙（墙足够长）围成一块留有一扇tm宽门的长方形花圃．设花圃宽AB为xm，面积为ym2，则y与x的函数表达式为y=-2x2+（24+t）x．
7．
如图，△ABC中，D为AB的中点，DE∥BC，则下列结论中错误的是（ ）
如图，△ABC中，D为AB的中点，DE∥BC，则下列结论中错误的是（ ）| A． | $\frac{AD}{BD}=\frac{DE}{BC}$ | B． | $\frac{AD}{BD}=\frac{AE}{EC}$ | ||
| C． | DE=$\frac{1}{2}$BC | D． | S△ADE=$\frac{1}{3}$S四边形BCED |
17．
如图，在△ABC中，点D、E分别是AB、C的中点，则S△ADE：S△ABC=（ ）
如图，在△ABC中，点D、E分别是AB、C的中点，则S△ADE：S△ABC=（ ）| A． | 1：2 | B． | 1：3 | C． | 1：4 | D． | 1：5 |
如图，已知正方形ABCD中，E为AD的中点，CF=3DF，求证：∠BEF为直角．
如图，二次函数y=-$\frac{1}{{m}^{2}}$x2-$\frac{2x}{m}$+3（其中m是常数，且m＞0）的图象与x轴交于A、B（点A位于点B的左侧），与y轴交于点C，作CD∥AB，点D在二次函数的图象上，连接BD，过点B作射线BE交二次函数的图象于点E，使得AB平分∠DBE．