题目内容
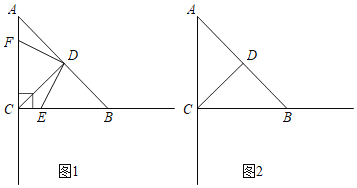
【题目】如图，在△ABC中，AD是高，E、F分别是AB、AC的中点．
（1）AB＝12，AC＝9，求四边形AEDF的周长；
（2）EF与AD有怎样的位置关系？证明你的结论．
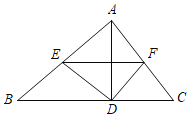
【答案】（1）21；（2）EF⊥AD，证明详见解析．
【解析】
(1)根据在直角三角形中，斜边上的中线等于斜边的一半可得ED=EB=
AB，DF=FC=AC，再由AB=12，AC=9，可得答案；
(2)根据到线段两端点距离相等的点在线段的垂直平分线证明．
(1)∵AD是高，
∴∠ADB=∠ADC=90°，
∵E、F分别是AB、AC的中点，
∴ED=EB=AB，DF=FC=AC，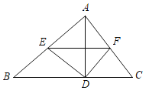
∵AB=12，AC=9，
∴AE+ED=12，AF+DF=9，
∴四边形AEDF的周长为12+9=21；
(2)EF⊥AD，
理由：∵DE=AE，DF=AF，
∴点E、F在线段AD的垂直平分线上，
∴EF⊥AD．
练习册系列答案
小学教材完全解读系列答案
相关题目
