Question

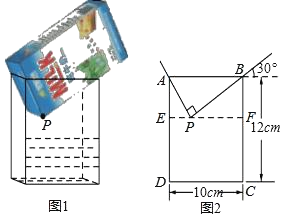
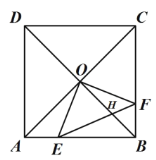
【题目】在边长为12的正方形中，对角线、交于点，点、分别为、边上的动点，且始终保持，连接交于点.

(1)求证：；

(2)若，求的值；

(3)在运动的过程中，是否存在最大值？若存在，请求出的最大值；若不存在，请说明理由.

Answer 1

【答案】(1)证明见解析；(2)；(3)存在最大值为18.

【解析】

（1）由正方形的性质可得OA=OB，∠OAE=∠OBF,再结合OE⊥OF可证明，进而证明△AOE≌△BOF；

（2）根据（1）得AE=BF，由勾股定理求得EF的值，过点作，垂足为点，得，故，求出EH和FH的值，即可得出结论；

（3）证明，得，设，则，得，故可求解.

(1)∵四边形是正方形，

∴，，，，，

∴，，，

∴，

∵，

∴，

∴，

∴，

∴.

(2)由(1)知，，

∴，

∵，，

∴，

∴，

∴，，

∴，

过点作，垂足为点，

∴，

∴，，

∴，，

∴，

∴.

设，则，，

∴，

∴，，

∴，

∴.

(3)由(1)知，，

∴，∴，∴，

又∵，

∴，∴，∴，

∵，∴，

设，则，

则，

即当时，有最大值为18，

即存在最大值为18.