Question

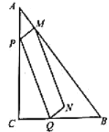
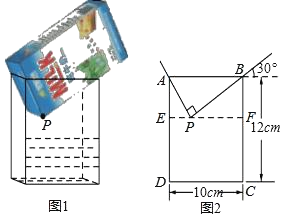
【题目】将一盒足量的牛奶按如图1所示倒入一个水平放置的长方体容器中，当容器中的牛奶刚好接触到点P时停止倒入，图2是它的平面示意图，请根据图中的信息解答下列问题：

（1）填空：AP＝　 　cm，PF＝　 　cm．

（2）求出容器中牛奶的高度CF．

Answer 1

【答案】（1）5，；（2）CF为（12﹣）cm．

【解析】

（1）解Rt△ABP，根据含30°角的直角三角形的性质得出AP=AB=5cm，求出EP=cm，即可求出PF；

（2）先由EF∥AB，得出∠BPF=∠ABP=30°，再解Rt△BFP，得出BF=cm，那么CF=BC-BF=（12-）cm．

解：（1）在Rt△ABP中，∵∠APB＝90°，∠ABP＝30°，AB＝10cm，

∴AP＝AB＝5cm，∠BAP＝60°；

∴∠EAP＝30°，

∴EP＝AP＝cm，

∴PF＝10﹣＝（cm）；

故答案为：5，；

（2）∵EF∥AB，

∴∠BPF＝∠ABP＝30°，

又∵∠BFP＝90°，

∴tan30°＝，

∴BF＝×＝（cm）．

∴CF＝BC﹣BF＝（12﹣）（cm）．

即容器中牛奶的高度CF为（12﹣）cm．