题目内容
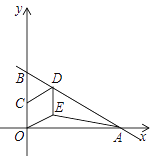
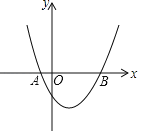
【题目】已知抛物线![]() 与
与![]() 轴交于点A和点B(3,0),与
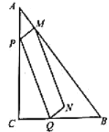
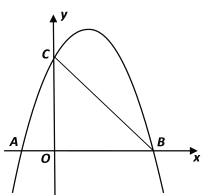
轴交于点A和点B(3,0),与![]() 轴交于点C(0,3),P是线段BC上一点,过点P作PN∥
轴交于点C(0,3),P是线段BC上一点,过点P作PN∥![]() 轴交
轴交![]() 轴于点N,交抛物线于点M.
轴于点N,交抛物线于点M.
(1)求该抛物线的表达式;
(2)如果点P的横坐标为2,点Q是第一象限抛物线上的一点,且△QMC和△PMC的面积相等,求点Q的坐标;
(3)如果![]() ,求tan∠CMN的值.
,求tan∠CMN的值.
【答案】(1)抛物线的表达式为![]() ;(2)点Q的坐标为(
;(2)点Q的坐标为(![]() ;(3)2.
;(3)2.
【解析】
试题(1)将B(3,0),C(0,3)代入y=-x2+bx+c,求得b、c的值,即可得该抛物线的表达式;(2)设直线BC的解析式为![]() ,把点C(0,3),B(3,0)代入,求得直线BC的解析式为
,把点C(0,3),B(3,0)代入,求得直线BC的解析式为![]() ,即可得P(2,1),M(2,3) 所以
,即可得P(2,1),M(2,3) 所以![]() ,设△QCM的边CM上的高为h,则
,设△QCM的边CM上的高为h,则![]() ,可得
,可得![]() ,即可得Q点的纵坐标为1,所以
,即可得Q点的纵坐标为1,所以![]() 解得
解得![]() ,即可得点Q的坐标为(
,即可得点Q的坐标为(![]() ;(3)过点C作
;(3)过点C作![]() ,垂足为H,设M
,垂足为H,设M![]() ,则P
,则P![]() ,因为
,因为![]() ,可得
,可得![]() ,由此可得
,由此可得![]() ,解得
,解得![]() ,即可得点P 的坐标为(
,即可得点P 的坐标为(![]() ,所以M
,所以M![]() ,求得
,求得![]() ,所以
,所以![]() .
.
试题解析:
(1)将![]() ,
,![]() 代入
代入![]() ,得
,得
![]() 解得
解得 ![]()
∴抛物线的表达式为![]()
(2)设直线BC的解析式为![]() ,把点C(0,3),B(3,0)代入得
,把点C(0,3),B(3,0)代入得
![]() ,解得
,解得 ![]() ∴直线BC的解析式为
∴直线BC的解析式为![]()
∴P(2,1),M(2,3)
∴![]() ,设△QCM的边CM上的高为h,则
,设△QCM的边CM上的高为h,则![]()
∴![]()
∴Q点的纵坐标为1,∴![]() 解得
解得![]()
∴点Q的坐标为(![]()
(3)过点C作![]() ,垂足为H
,垂足为H
设M![]() ,则P
,则P![]()
∵![]() ,∴
,∴![]() ,∴
,∴![]()
解得![]() ,∴点P 的坐标为(
,∴点P 的坐标为(![]()
∴M![]()
∴![]() ,∴
,∴![]()

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案【题目】好街坊橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
进价(元/台) | 售价(元/台) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,橱具店购进这两种电器共 30 台,用去了 5520 元,并且全部售完,问橱具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过 8850 元的资金采购电饭煲和电压锅共 50 台,且电饭煲的利润不少于电压锅的利润的![]() ,问橱具店有哪几种进货方案?并说明理由;
,问橱具店有哪几种进货方案?并说明理由;
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?