题目内容
10、如图，P为Rt△ABC斜边AB上任意一点（除A、B外），过点P作直线截△ABC，使截得的新三角形与△ABC相似，满足这样条件的直线的作法共有（ ）分析：根据已知及相似三角形的判定方法进行分析，从而得到最后答案．
解答：
解：过点P可作PE∥BC或PE∥AC，可得相似三角形；
过点P还可作PE⊥AB，可得：∠EPA=∠C=90°，∠A=∠A
∴△APE∽△ACB；
∴共有3条．
解：过点P可作PE∥BC或PE∥AC，可得相似三角形；过点P还可作PE⊥AB，可得：∠EPA=∠C=90°，∠A=∠A
∴△APE∽△ACB；
∴共有3条．
点评：此题考查了相似三角形的判定：
①有两个对应角相等的三角形相似；
②有两个对应边的比相等，且其夹角相等，则两个三角形相似；
③三组对应边的比相等，则两个三角形相似．
①有两个对应角相等的三角形相似；
②有两个对应边的比相等，且其夹角相等，则两个三角形相似；
③三组对应边的比相等，则两个三角形相似．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
6、如图，CD为Rt△ABC斜边上的高，∠BAC的平分线分别交CD、CB于点E、F，FG⊥AB，垂足为G，则CF
15、如图，D为Rt△ABC中斜边BC上的一点，且BD=AB，过D作BC的垂线，交AC于E，若AE=12cm，则DE的长为
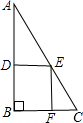如图，E为Rt△ABC斜边上一点，四边形BFED为正方形，若BC=6，AB=8，则正方形BFED的边长为（ ）A、
| ||
B、
| ||
| C、4 | ||
| D、3 |
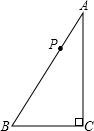如图，P为Rt△ABC斜边AB上任意一点（除A、B外），过点P作直线截△ABC，使截得的新三角形与△ABC相似，满足这样条件的直线的作法共有
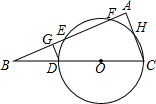如图，D为Rt△ABC斜边BC上的一点，以CD为直径作⊙O交边AB于E、F两点，交AC于H，DG⊥AB于点G