题目内容
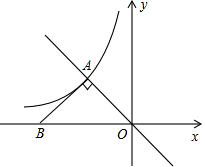 如图,点A是正比例函数y=-x与反比例函数y=
如图,点A是正比例函数y=-x与反比例函数y=| k | x |
-4
-4
.分析:过点A作AC⊥OB于C,先由正比例函数的性质及AB⊥OA,得出△AOB是等腰直角三角形,根据等腰三角形三线合一的性质得出BC=OC,则S△AOC=
S△AOB=2,再根据反比例函数的性质可以得到△AOC的面积等于|k|的一半,由此求解即可.
| 1 |
| 2 |
解答: 解:过点A作AC⊥OB于C.
解:过点A作AC⊥OB于C.
∵点A是正比例函数y=-x与反比例函数y=
在第二象限的交点,AB⊥OA交x轴于点B,
∴△AOB是等腰直角三角形,
∴BC=OC,
∴S△AOC=
S△AOB=2,即
|k|=2,
∴k=±4,
∵反比例函数y=
的图象在在第二象限,
∴k<0,
∴k=-4.
故答案为-4.
 解:过点A作AC⊥OB于C.
解:过点A作AC⊥OB于C.∵点A是正比例函数y=-x与反比例函数y=
| k |
| x |
∴△AOB是等腰直角三角形,
∴BC=OC,
∴S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴k=±4,
∵反比例函数y=
| k |
| x |
∴k<0,
∴k=-4.
故答案为-4.
点评:本题考查反比例系数k的几何意义,过双曲线上的任意一点分别向两条坐标作垂线,与坐标轴围成的矩形面积就等于|k|.该知识点是中考的重要考点,同学们应高度关注.同时考查了正比例函数的性质,等腰三角形的性质.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
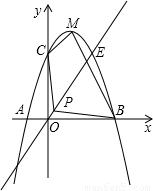
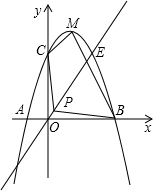 顶点为M,又正比例函数y=kx的图象于二次函数相交于两点D、E,且P是线段DE的中点.
顶点为M,又正比例函数y=kx的图象于二次函数相交于两点D、E,且P是线段DE的中点.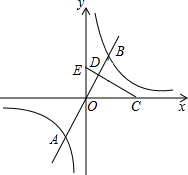 如图,已知正比例函数y=ax(a≠0)的图象与反比例函致
如图,已知正比例函数y=ax(a≠0)的图象与反比例函致 为M,又正比例函数y=kx的图象与二次函数相交于两点D、E,且P是线段DE的中点.
为M,又正比例函数y=kx的图象与二次函数相交于两点D、E,且P是线段DE的中点. 】
】
 (k≠0)的图象的一个交点为A(-1,2-k2),另—个交点为B,且A、B关于原点O对称,D为OB的中点,过点D的线段OB的垂直平分线与x轴、y轴分别交于C、E.
(k≠0)的图象的一个交点为A(-1,2-k2),另—个交点为B,且A、B关于原点O对称,D为OB的中点,过点D的线段OB的垂直平分线与x轴、y轴分别交于C、E.