题目内容
 如图,AB是⊙O的直径,AB=d,过A作⊙O的切线并在其上取一点C,使AC=AB,连接OC交⊙O于点D,BD的延长线交AC于E.
如图,AB是⊙O的直径,AB=d,过A作⊙O的切线并在其上取一点C,使AC=AB,连接OC交⊙O于点D,BD的延长线交AC于E.(1)求证:CD=AE;
(2)求AE的长.
考点:相似三角形的判定与性质,解一元二次方程-公式法,圆周角定理
专题:计算题,证明题
分析:易证△CDE∽△CAD进而求证
=
,再根据AB=AC,可得AE=CD;
(2)由△CDE∽△CAD可得
=
,设AE=x,则CE=d-x,于是x2=d(d-x),解x的值即可解题.
| CD |
| AC |
| AE |
| AB |
(2)由△CDE∽△CAD可得
| CD |
| CA |
| CE |
| CD |
解答: (1)证明:如图,连接AD,
(1)证明:如图,连接AD,
∵OB=OD,∴∠B=∠ODB,
∵∠ADO+∠ODB=90°,∠B+∠OAD=90°,
∴∠OAD+∠B=90°,∴∠CAD=∠B,
∴CAD=∠ODB=∠EDC,又∵∠C=∠C,
∴△CDE∽△CAD,
∴
=
①
又∵△ADE∽△BDA
∴
=
②
由①、②得
=
又∵AB=AC,可得AE=CD
(2)解:又由△CDE∽△CAD可得
=
,
即AE2=CD2=CE×CA
设AE=x,则CE=d-x,于是x2=d(d-x)
即有AE=x=
d(负值已舍去)
 (1)证明:如图,连接AD,
(1)证明:如图,连接AD,∵OB=OD,∴∠B=∠ODB,
∵∠ADO+∠ODB=90°,∠B+∠OAD=90°,
∴∠OAD+∠B=90°,∴∠CAD=∠B,
∴CAD=∠ODB=∠EDC,又∵∠C=∠C,
∴△CDE∽△CAD,
∴
| CD |
| AC |
| DE |
| AD |
又∵△ADE∽△BDA
∴
| DE |
| AD |
| AE |
| AB |
由①、②得
| CD |
| AC |
| AE |
| AB |
又∵AB=AC,可得AE=CD
(2)解:又由△CDE∽△CAD可得
| CD |
| CA |
| CE |
| CD |
即AE2=CD2=CE×CA
设AE=x,则CE=d-x,于是x2=d(d-x)
即有AE=x=
| ||
| 2 |
点评:本题考查了相似三角形的证明,考查了相似三角形对应边相等的性质,考查了一元二次方程的求解,本题中求△CDE∽△CAD是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
用10根长度相同的木棍拼成一个三角形(不剩余木棍也不折断木棍),则只能拼成( )
| A、直角三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
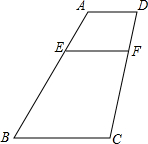 如图,梯形ABCD中,AD∥BC,E为线段AB上的点,且满足AE=AD,BE=BC,过E作EF∥BC交CD于F,设P为线段CD上任意一点,试说明
如图,梯形ABCD中,AD∥BC,E为线段AB上的点,且满足AE=AD,BE=BC,过E作EF∥BC交CD于F,设P为线段CD上任意一点,试说明 将长为12,宽为5的矩形纸片沿对角线对折后放在桌面上,那么它覆盖的桌面的面积等于
将长为12,宽为5的矩形纸片沿对角线对折后放在桌面上,那么它覆盖的桌面的面积等于 (Figure 1)In the parallelogram ABCD,AD=2AB,a point M is mid-point of segment AD,CE⊥AB,if∠CEM=40°,then the value of∠DME is( )
(Figure 1)In the parallelogram ABCD,AD=2AB,a point M is mid-point of segment AD,CE⊥AB,if∠CEM=40°,then the value of∠DME is( )