题目内容
如图，边长为8的正方形ABCD中，E为CD边上一点，且DE=2，M是对角线AC上的一个动点，则DM+EM的最小值为________．
10
分析：首先连接BD，连接BE交AC于M，根据正方形的性质推出D、B关于AC对称，求出DM+ME=BE，在△BCE中由勾股定理求出BM即可．
解答：
解：连接BD交AC于O，
∵四边形ABCD是正方形，
∴AC⊥BD，OD=OB，
即D、B关于AC对称，
∴DM=BM，
连接BE交AC于M，则此时DM+ME最小，
∴DM=BM，
∴DM+ME=BM+ME=BE，
∵四边形ABCD是正方形，
∴∠BCD=90°，BC=8，CE=8-2=6，
由勾股定理得：BE=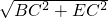
=10，
∴DM+ME=BE=10．
故答案为：10．
点评：本题主要考查对正方形的性质，勾股定理，轴对称-最短路线问题等知识点的理解和掌握，能求出DM+ME=BM+ME=BE和BE的长是解此题的关键．
分析：首先连接BD，连接BE交AC于M，根据正方形的性质推出D、B关于AC对称，求出DM+ME=BE，在△BCE中由勾股定理求出BM即可．
解答：
解：连接BD交AC于O，∵四边形ABCD是正方形，
∴AC⊥BD，OD=OB，
即D、B关于AC对称，
∴DM=BM，
连接BE交AC于M，则此时DM+ME最小，
∴DM=BM，
∴DM+ME=BM+ME=BE，
∵四边形ABCD是正方形，
∴∠BCD=90°，BC=8，CE=8-2=6，
由勾股定理得：BE=
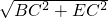=10，∴DM+ME=BE=10．
故答案为：10．
点评：本题主要考查对正方形的性质，勾股定理，轴对称-最短路线问题等知识点的理解和掌握，能求出DM+ME=BM+ME=BE和BE的长是解此题的关键．
练习册系列答案
天天练口算系列答案
相关题目
如图，边长为6的正方OABC的顶点O在坐标原点处，点A、C分别在x轴、y轴的正半轴上，点E是OA边上的点（不与点A重合），EF⊥CE，且与正方形外角平分线AC交于点P．
如图，边长为6的正方OABC的顶点O在坐标原点处，点A、C分别在x轴、y轴的正半轴上，点E是OA边上的点（不与点A重合），EF⊥CE，且与正方形外角平分线AC交于点P．
轴正方向连续翻转2006次，点P依次落在点
，
，
，
，……
的位置，则
＝_________．
