题目内容
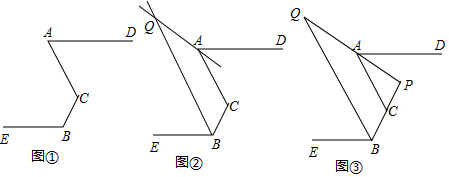
9．一个抽屉内壁的长、宽、高分别是32cm，24cm，9cm，要把一个长42cm的画轴放入抽屉，能不能放进去（画轴半径忽略不计）？为什么？分析 根据题意画出图形，再由勾股定理求出CF的长与画轴的长进行比较即可．
解答 
解：画轴不能放入抽屉．
理由：连接FH、CF，在Rt△FGH中，
FH=$\sqrt{F{G}^{2}+G{H}^{2}}$=$\sqrt{2{4}^{2}+3{2}^{2}}$=40（cm），
在Rt△CFH中，
CF=$\sqrt{C{H}^{2}+F{H}^{2}}$=$\sqrt{4{0}^{2}+{9}^{2}}$=41cm＜42cm．
故画轴不能放入抽屉．
点评 本题考查的是勾股定理在实际生活中的应用，解答此题的关键是根据题意画出图形，再利用勾股定理求解．
练习册系列答案
相关题目
如图，已知直线EF交x轴于点E（18，0），交y轴于点F，∠FEO=30°，C、D为EF上两点，且两点的横坐标分别为12和6；DA⊥y轴于点A，CB⊥y轴于点B，CQ⊥x轴于点Q．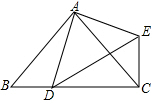
如图，在△ABC中，AB=AC，点D在线段BC上运动，连接AD，以AD为边作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．
如图所示，四边形ABCD是张大爷的一块小菜地，已知AD⊥AB，AD⊥CD，AD=$\sqrt{3}$，BC=CD=2$\sqrt{3}$，请帮张大爷计算一下这个四边形菜地的周长和面积．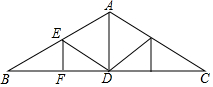
如图是屋顶的“人字形”钢架，其中斜梁AB=AC，顶角∠BAC=120°，立柱AD⊥BC，EF⊥BC，DE∥AC，AB=8m，则EF=2m．
1．a、b、c是三角形的三边长，且（a+b）2=c2+2ab，则这个三角形是（ ）
| A． | 锐角三角形 | B． | 直角三角形 | C． | 钝角三角形 | D． | 等边三角形 |
