题目内容
5.计算:(1-$\frac{1}{1-{2}^{2}}$)(1-$\frac{1}{1-{3}^{2}}$)(1$-\frac{1}{1-{4}^{2}}$)…(1-$\frac{1}{1-{9}^{2}}$)(1-$\frac{1}{1-1{0}^{2}}$).分析 首先通分,计算后再进一步利用平方差公式因式分解,交错约分得出答案即可.
解答 解:原式=$\frac{{2}^{2}}{(2+1)(2-1)}$×$\frac{{3}^{2}}{(3-1)(3+1)}$×$\frac{{4}^{2}}{(4-1)(4+1)}$×…×$\frac{{9}^{2}}{(9-1)(9+1)}$×$\frac{1{0}^{2}}{(10-1)(10+1)}$
=$\frac{{2}^{2}}{1×3}$×$\frac{{3}^{2}}{2×4}$×$\frac{{4}^{2}}{3×5}$×…×$\frac{{9}^{2}}{8×10}$×$\frac{1{0}^{2}}{9×11}$
=$\frac{2×10}{11}$
=$\frac{20}{11}$.
点评 此题考查因式分解的实际运用,有理数的混合运算,利用平方差公式因式分解是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
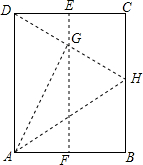 矩形ABCD中,E,F分别是CD,AB中点,连EF,沿AH折叠,B落在EF的G处,HG的延长线过D,证明:△AHD为等边三角形.
矩形ABCD中,E,F分别是CD,AB中点,连EF,沿AH折叠,B落在EF的G处,HG的延长线过D,证明:△AHD为等边三角形.