题目内容
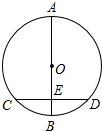如图，AB是⊙O的直径，CD是弦，AB⊥CD于点E，若半径为5，OE=3，则CD的长是（ ）| A、4 | B、6 | C、8 | D、7 |
考点：垂径定理,勾股定理
专题：
分析：连接OC，先根据垂径定理得出CE=
CD，在Rt△OCE中根据勾股定理求出CE的长，进而可得出结论．
| 1 |
| 2 |
解答：
解：∵AB是⊙O的直径，CD是弦，AB⊥CD于点E，
∴CE=
CD．
在Rt△OCE中，
∵OC=5，OE=3，
∴CE=
=
=4，
∴CD=2CE=8．
故选C．
解：∵AB是⊙O的直径，CD是弦，AB⊥CD于点E，∴CE=
| 1 |
| 2 |
在Rt△OCE中，
∵OC=5，OE=3，
∴CE=
| OC2-OE2 |
| 52-32 |
∴CD=2CE=8．
故选C．
点评：本题考查的是垂径定理及勾股定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．
练习册系列答案
相关题目
点A（5，y1）和B（2，y2）都在直线y=-x上，则y1与y2的关系是（ ）
| A、y1≥y2 |
| B、y1=y2 |
| C、y1＜y2 |
| D、y1＞y2 |
已知OA⊥OB，O为垂足，且∠AOC：∠AOB=1：2，则∠BOC是（ ）
| A、45° |
| B、135° |
| C、45°或135° |
| D、60°或20° |
数据0、1、2、3的标准差是（ ）
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
小敏从A地出发向B地行走，同时小聪从B地出发向 A地行走，如图所示，相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离ykm与已用时间x h之间的关系，则小敏、小聪行走的速度分别是（ ）| A、3m/h和4km/h |
| B、3km/h和3km/h |
| C、4km/h和4km/h |
| D、4km/h和3km/h |
在代数式x2+5，-1，x2-3x+2，π，
，x2+
x2中，单项式有（ ）
| 5 |
| x |
| 1 |
| x+1 |
| A、1个 | B、2个 | C、3个 | D、4个 |