Question

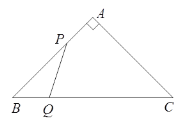
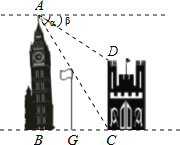
【题目】如图所示，在两建筑物之间有一高为15米的旗杆，从高建筑物的顶端A点经过旗杆顶点恰好看到矮建筑物的底端墙角C点，且俯角a为60°，又从A点测得矮建筑物左上角顶端D点的俯角β为30°，若旗杆底部点G为BC的中点（点B为点A向地面所作垂线的垂足）则矮建筑物的高CD为_____．

Answer 1

【答案】20米

【解析】

根据点G是BC中点，可判断EG是△ABC的中位线，求出AB，在Rt△ABC和在Rt△AFD中，利用特殊角的三角函数值分别求出BC、DF，继而可求出CD的长度．

解：过点D作DF⊥AF于点F，

∵点G是BC中点，EG∥AB，

∴EG是△ABC的中位线，

∴AB＝2EG＝30米，

在Rt△ABC中，∵∠CAB＝30°，

∴BC＝ABtan∠BAC＝30×＝10米．

在Rt△AFD中，∵AF＝BC＝10米，

∴FD＝AFtanβ＝10×＝10米，

∴CD＝AB﹣FD＝30﹣10＝20米．

故答案为：20米．