题目内容
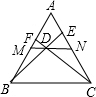如图，在等边△ABC中，M、N分别是AB、AC的中点，D为MN上任意一点，BD、CD的延长线分别交AC、AB于点E、F，若| 1 |
| CE |
| 1 |
| BF |
分析：可过点D作DS∥BM，DT∥CN，由平行线的性质可得
=
，
=
，进而再结合题中已知条件即可求解．
| DS |
| BF |
| SC |
| BC |
| DT |
| CE |
| BT |
| BC |
解答：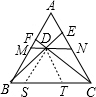
解：过点D作DS∥BM，DT∥CN交BC于S、T，
易证MDSB、NDTC都是平行四边形，
△DST是等边三角形，DS=ST=DT，
由DS∥BM?
=
，
∴
=
，
由DT∥CN?
=
，
∴
=
，
∴
+
=
=
=
，
∴3BC=3，BC=1，
∴S△ABC=
．
故答案为：
．
解：过点D作DS∥BM，DT∥CN交BC于S、T，易证MDSB、NDTC都是平行四边形，
△DST是等边三角形，DS=ST=DT，
由DS∥BM?
| DS |
| BF |
| SC |
| BC |
∴
| 1 |
| BF |
| SC |
| BC×DS |
由DT∥CN?
| DT |
| CE |
| BT |
| BC |
∴
| 1 |
| CE |
| BT |
| BC×DT |
∴
| 1 |
| CE |
| 1 |
| BF |
| CS+BT |
| BC•ST |
| ||
BC•
|
| 3 |
| BC |
∴3BC=3，BC=1，
∴S△ABC=
| ||
| 4 |
故答案为：
| ||
| 4 |
点评：本题主要考查了平行线分线段成比例的性质，能够利用其性质求解一些简单的计算问题．
练习册系列答案
相关题目
16、如图，在等边△ABC的边BC上任取一点D，作∠ADE=60°，DE交∠C的外角平分线于E，则△ADE是
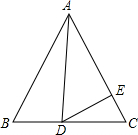如图，在等边△ABC中，D为BC边上一点，E为AC边上一点，且∠ADE=60°，BD=3，CE=2，则△ABC的面积为（ ）A、81
| ||||
B、
| ||||
C、
| ||||
D、
|
21、如图，在等边△ABC中，AD是∠BAC的平分线，点E在AC边上，且∠EDC=15°．
如图，在等边△ABC中，D是AC的中点，延长BC到点E，使CE=CD，AB=10cm．
如图，在等边△ABC中，BF是高，D是BF上一点，且OF=AF，作OE⊥BF，垂足为D，且OE=OB，连AE、AO、BE，求证：