题目内容
2. 按要求完成下列各小题.
按要求完成下列各小题.(1)解方程:x2+6x+2=2x+7;
(2)如图是反比例函数y=$\frac{2k}{x}$在第三象限的图案,点M在该图象上,且点M到点x轴,y轴的距离都等于|k|,求k的值.
分析 (1)先把方程化为一元二次方程的一般形式,再用因式分解法求出x的值即可;
(2)根据函数图象在第三象限得出2k>0,再由点M到点x轴,y轴的距离都等于|k|可设M(-k,-k),代入反比例函数的解析式即可得出结论.
解答 解:(1)原方程可化为x2+4x-5=0,即(x-1)(x+5)=0,解得x1=1,x2=-5;
(2)∵函数图象在第三象限,
∴2k>0,即k>0.
∵点M到点x轴,y轴的距离都等于|k|,
∴设M(-k,-k),
∴(-k)2=2k,解得k=2.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
10.在$\frac{1}{x}$,$\frac{1}{2}$,$\frac{x+1}{2}$,$\frac{xy}{π}$,$\frac{3}{x+y}$中,分式的个数为( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
17.如果弧长为6π的弧所对的圆心角为60°,那么这条弧所在的圆的半径是( )
| A. | 18 | B. | 12 | C. | 36 | D. | 6 |
7.下列个数中,负数是( )
| A. | 5 | B. | 0.56 | C. | -3 | D. | +9 |
11.为了鼓励居民节约用水,万源市民生给排水公司对居民生活用水按阶梯式水价计费,下表是我市居民“一户一表”生活用水阶梯式计费价格表的一部分信息:
[说明:①每户产生的污水量等于该户的用水量;②水费=自来水费+污水处理费]
(1)已知小李家2013年4月份用水量16吨,交水费45.2元;5月份用水量14吨,交水费37.9元.求表中a、b的值.
(2)设小李家每月用水量为x吨,交水费y元,求y(元)与x(吨)的函数关系式,并指出自变量x的取值范围.
| 自来水销售价格 | 污水处理价格 | |
| 每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
| 12吨以下(含12吨) | a | 0.15 |
| 超过12吨不超过18吨的部分 | b | |
| 超过18吨的部分 | 4.5 | |
(1)已知小李家2013年4月份用水量16吨,交水费45.2元;5月份用水量14吨,交水费37.9元.求表中a、b的值.
(2)设小李家每月用水量为x吨,交水费y元,求y(元)与x(吨)的函数关系式,并指出自变量x的取值范围.
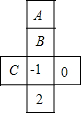 如图所示,这是一个正方体纸盒的展开图,若在其中的三个正方形A、B、C内分别填入适当的数,使得它们在折成正方形后相对的面上的两个数互为相反数,则A+B+C的值是-1.
如图所示,这是一个正方体纸盒的展开图,若在其中的三个正方形A、B、C内分别填入适当的数,使得它们在折成正方形后相对的面上的两个数互为相反数,则A+B+C的值是-1.