题目内容
1.(1)如图①,你知道∠BOC=∠B+∠C+∠A的奥秘吗?请用你学过的知识予以证明;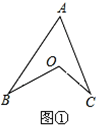
(2)如图②,设x=∠A+∠B+∠C+∠D+∠E,运用(1)中的结论填空.
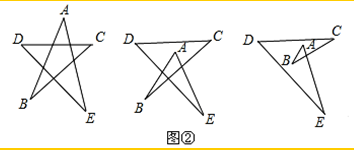
x=180°; x=180°; x=180°;
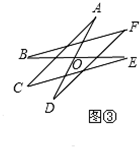
(3)如图③,一个六角星,其中∠BOD=70°,则:∠A+∠B+∠C+∠D+∠E+∠F=140°.
分析 (1)首先延长BO交AC于点D,可得BOC=∠BDC+∠C,然后根据∠BDC=∠A+∠B,判断出∠BOC=∠B+∠C+∠A即可.
(2)a、首先根据外角的性质,可得∠1=∠A+∠B,∠2=∠C+∠D,然后根据∠1+∠2+∠E=180°,可得x=∠A+∠B+∠C+∠D+∠E=180,据此解答即可.
b、首先根据外角的性质,可得∠1=∠A+∠B,∠2=∠C+∠D,然后根据∠1+∠2+∠E=180°,可得x=∠A+∠B+∠C+∠D+∠E=180,据此解答即可.
c、首先延长EA交CD于点F,EA和BC交于点G,然后根据外角的性质,可得∠GFC=∠D+∠E,∠FGC=∠A+∠B,再根据∠GFC+∠FGC+∠C=180°,可得x=∠A+∠B+∠C+∠D+∠E=180°,据此解答即可.
(3)根据∠BOD=70°,可得∠A+∠C+∠E=70°,∠B+∠D+∠F=70°,据此求出∠A+∠B+∠C+∠D+∠E+∠F的度数是多少即可.
解答 解:(1)如图①,延长BO交AC于点D,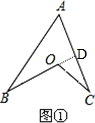
∠BOC=∠BDC+∠C,
又∵∠BDC=∠A+∠B,
∴∠BOC=∠B+∠C+∠A.
(2)如图②,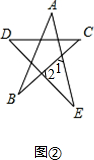 ,
,
根据外角的性质,可得
∠1=∠A+∠B,∠2=∠C+∠D,
∵∠1+∠2+∠E=180°,
∴x=∠A+∠B+∠C+∠D+∠E=180°.
如图③,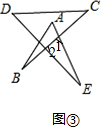 ,
,
根据外角的性质,可得
∠1=∠A+∠B,∠2=∠C+∠D,
∵∠1+∠2+∠E=180°,
∴x=∠A+∠B+∠C+∠D+∠E=180°.
如图④,延长EA交CD于点F,EA和BC交于点G,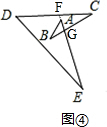 ,
,
根据外角的性质,可得
∠GFC=∠D+∠E,∠FGC=∠A+∠B,
∵∠GFC+∠FGC+∠C=180°,
∴x=∠A+∠B+∠C+∠D+∠E=180°.
(3)如图⑤,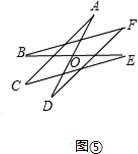 ,
,
∵∠BOD=70°,
∴∠A+∠C+∠E=70°,
∴∠B+∠D+∠F=70°,
∴∠A+∠B+∠C+∠D+∠E+∠F=70°+70°=140°.
故答案为:180、180、180、140.
点评 (1)此题主要考查了三角形的内角和定理,要熟练掌握,解答此题的关键是要明确:三角形的内角和是180°.
(2)此题还考查了三角形的外角的性质和应用,要熟练掌握,解答此题的关键是要明确:①三角形的外角和为360°.②三角形的一个外角等于和它不相邻的两个内角的和.③三角形的一个外角大于和它不相邻的任何一个内角.

 单元期中期末卷系列答案
单元期中期末卷系列答案| A. | 6 | B. | -6 | C. | ±6 | D. | 18 |
 如图,不能判定AB∥DF的是( )
如图,不能判定AB∥DF的是( )| A. | ∠1=∠2 | B. | ∠A=∠4 | C. | ∠1=∠A | D. | ∠A+∠3=180° |
 如图,有一个与地面成30°角的斜坡,现要在斜坡上竖一电线杆,当电线杆与地面垂直时,它与斜坡所成的角α=60°.
如图,有一个与地面成30°角的斜坡,现要在斜坡上竖一电线杆,当电线杆与地面垂直时,它与斜坡所成的角α=60°.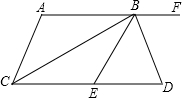 如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:
如图,AF∥CD,CB平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论: 某宾馆铺地毯,已知主楼梯宽3米,其余数据如图所示,需购地毯多少平方米?
某宾馆铺地毯,已知主楼梯宽3米,其余数据如图所示,需购地毯多少平方米?