题目内容
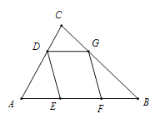
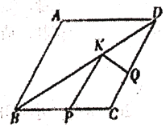
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() ,
,![]() 上的任意一点,则
上的任意一点,则![]() 的最小值为__________.
的最小值为__________.
【答案】![]()
【解析】
根据菱形的对称性,在AB上找到点P关于BD的对称点![]() ,过点
,过点![]() 作
作![]() Q⊥CD于Q,交BD于点K,连接PK,过点A作AE⊥CD于E,根据垂线段最短和平行线之间的距离处处相等,可得此时
Q⊥CD于Q,交BD于点K,连接PK,过点A作AE⊥CD于E,根据垂线段最短和平行线之间的距离处处相等,可得此时![]() 最小,且最小值为
最小,且最小值为![]() 的长,
的长,![]() ,然后利用锐角三角函数求AE即可.
,然后利用锐角三角函数求AE即可.
解:根据菱形的对称性,在AB上找到点P关于BD的对称点![]() ,过点
,过点![]() 作
作![]() Q⊥CD于Q,交BD于点K,连接PK,过点A作AE⊥CD于E
Q⊥CD于Q,交BD于点K,连接PK,过点A作AE⊥CD于E
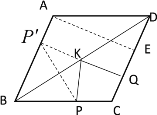
根据对称性可知:PK=![]() K,
K,
∴此时![]() =
=![]() ,根据垂线段最短和平行线之间的距离处处相等,
,根据垂线段最短和平行线之间的距离处处相等,
∴此时![]() 最小,且最小值为
最小,且最小值为![]() 的长,
的长,![]()
∵在菱形![]() 中,
中,![]() ,
,![]()
∴![]() ,∠ADE=180°-∠A=60°
,∠ADE=180°-∠A=60°
在Rt△ADE中,AE=AD·sin∠ADE=![]()
∴![]()
即![]() 的最小值为
的最小值为![]()
故答案为![]() .
.

练习册系列答案
相关题目