题目内容
9.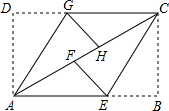 如图,ABCD是矩形纸片,翻折∠B、∠D,使点B、D恰好落在AC边上的点F、H处,CE与AG为折痕.
如图,ABCD是矩形纸片,翻折∠B、∠D,使点B、D恰好落在AC边上的点F、H处,CE与AG为折痕.(1)证明:四边形AECG是平行四边形;
(2)连接GF、HE,判断四边形GFEH的形状.
分析 (1)由四边形ABCD是矩形,可得AD∥BC,AB∥CD,又由平行线的性质,可得∠DAC=∠BCA,然后根据折叠的性质可得:∠1=$\frac{1}{2}$∠DAC,∠2=$\frac{1}{2}$∠BCA,即可证得AG∥CE,根据有两组对边分别平行的四边形是平行四边形,即可证得四边形AECG是平行四边形.
(2)证明△ADG≌△CBE得出GH∥EF,GH∥EF继而可判断四边形GFEH的形状.
解答 (1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AB∥CD,
∴∠DAC=∠BCA,
由折叠的性质可得:∠GAH=$\frac{1}{2}$∠DAC,∠ECF=$\frac{1}{2}$∠BCA,
∴∠GAH=∠ECF,
∴AG∥CE,
∴四边形AECG是平行四边形.
(2)解:四边形GFEH是平行四边形;理由如下:如图所示: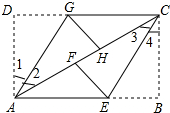
根据题意可知:GH⊥AC,EF⊥AC
∴EF∥GH,
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,∠D=∠B=90°,
∴∠1+∠2=∠3+∠4,
由折叠可知,∠1=∠2,∠3=∠4,DG=GH,BE=EF,
∴∠1=∠4,
在△ADG和△CBE中,$\left\{\begin{array}{l}{∠D=∠B}&{\;}\\{AD=CB}&{\;}\\{∠1=∠4}&{\;}\end{array}\right.$,
∴△ADG≌△CBE(ASA),
∴DG=BE,
∴GH=EF,
∴GH∥EF,GH=EF,
∴四边形GFEH是平行四边形.
点评 本题考查了矩形的性质、翻折变换的性质、平行四边形的判定、全等三角形的判定与性质;熟练掌握矩形和翻折变换的性质,证明三角形全等是解决问题(2)的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.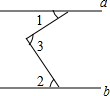 如图,已知直线a∥b,∠1=30°,∠2=50°,则∠3等于( )
如图,已知直线a∥b,∠1=30°,∠2=50°,则∠3等于( )
 如图,已知直线a∥b,∠1=30°,∠2=50°,则∠3等于( )
如图,已知直线a∥b,∠1=30°,∠2=50°,则∠3等于( )| A. | 20° | B. | 80° | C. | 100° | D. | 90° |
18.x取下列各数中的哪个数时,二次根式$\sqrt{x-5}$有意义( )
| A. | -3 | B. | 0 | C. | 3 | D. | 6 |
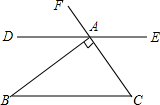 如图,BA⊥FC于A点,过A点作DE∥BC,若∠EAF=125°,则∠B=35°.
如图,BA⊥FC于A点,过A点作DE∥BC,若∠EAF=125°,则∠B=35°.