Question

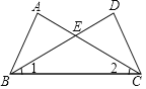
【题目】已知：如图，△ABC中，AC⊥BD于C，=，E是AB的中点，tanD=2，CE=1，求sin∠ECB和AD的长．

Answer 1

【答案】sin∠ECB=，AD=．

【解析】

试题由直角三角形斜边上的中线等于斜边的一半，得到AB=2，设BC=3x，则CD=2x．AC=4x，在Rt△ACB中由勾股定理AB=5x，由∠ECB=∠B，求出sin∠ECB及x的值，在Rt△ACD中，由勾股定理求得AD的长．

试题解析：∵AC⊥BD，∴∠ACB=∠ACD=90°，∵E是AB的中点，CE=1，∴AB=2CE=2，∵∴设BC=3x，CD=2x，在Rt△ACD中，tanD=2，∴，AC=4x，在Rt△ACB中由勾股定理AB=5x，∴sin∠ECB=sinB=，由AB=2，得，∴．