题目内容
15.用适当的方法解下列方程:(1)4(2x+1)2-9=0;
(2)x2+4x-2=0;
(3)2x2-7x+3=0;
(4)(x+1)(x-1)+2(x+3)=8.
分析 (1)先变形得到(2x+1)2=$\frac{9}{4}$,然后利用直接开平方法解方程;
(2)利用配方法得到(x+2)2=6,然后利用直接开平方法解方程;
(3)利用因式分解法解方程;
(4)利用因式分解法解方程.
解答 解:(1)(2x+1)2=$\frac{9}{4}$
2x+1=±$\frac{3}{2}$,
所以x1=$\frac{1}{4}$,x2=-$\frac{5}{4}$;
(2)x2+4x+4=6,
(x+2)2=6,
x+2=±$\sqrt{6}$,
所以x1=-2+$\sqrt{6}$,x2=-2-$\sqrt{6}$;
(3)(2x-1)(x-3)=0,
2x-1=0或x-3=0,
所以x1=$\frac{1}{2}$,x2=3;
(4)x2+2x-3=0,
(x+3)(x-1)=0,
x+3=0或x-1=0,
所以x1=-3,x2=1.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了配方法解一元二次方程.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 如图,点P关于OA,OB的对称点分别为C、D,连接CD,交OA于M,交OB于N,若△PMN的周长为10cm,则CD的长为10cm.
如图,点P关于OA,OB的对称点分别为C、D,连接CD,交OA于M,交OB于N,若△PMN的周长为10cm,则CD的长为10cm.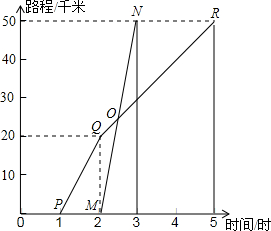 如图所示,A、B两地相距50千米.甲于某日下午1时骑自行车从A地驶往B地,乙也于同日下午骑摩托车按同路从A地出发出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午时间t之间的关系.
如图所示,A、B两地相距50千米.甲于某日下午1时骑自行车从A地驶往B地,乙也于同日下午骑摩托车按同路从A地出发出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午时间t之间的关系.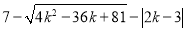 的结果是( )
的结果是( )