��Ŀ����
20��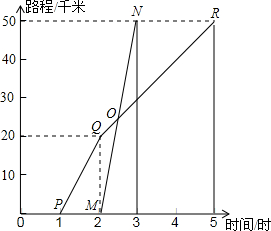 ��ͼ��ʾ��A��B�������50ǧ�ף�����ij������1ʱ�����г���A��ʻ��B�أ���Ҳ��ͬ��������Ħ�г���ͬ·��A�س�������ʻ��B�أ���ͼ��ʾ��ͼ�е�����PQR���߶�MN�ֱ��ʾ�ס�������ʻ��·��S���������ʱ��t֮��Ĺ�ϵ��
��ͼ��ʾ��A��B�������50ǧ�ף�����ij������1ʱ�����г���A��ʻ��B�أ���Ҳ��ͬ��������Ħ�г���ͬ·��A�س�������ʻ��B�أ���ͼ��ʾ��ͼ�е�����PQR���߶�MN�ֱ��ʾ�ס�������ʻ��·��S���������ʱ��t֮��Ĺ�ϵ����1���׳���1Сʱ��ʻ��20ǧ�ף�֮��2Сʱ��ʻ���ٶ���10ǧ��/ʱ������ʻ���ٶ���50ǧ��/ʱ
��2���׳����ʱ������ϣ�
��3�������ӵ�ʱ���������10ǧ�ף�
���� ��1����ͼ��֪���׳���1Сʱ��ʻ��20ǧ�ף�֮��ʱ��Ϊ3Сʱ��·��Ϊ30ǧ�ף��Ӷ��ó��ٶȣ��Ҵ�A�ص�B������ʱ��Ϊ1Сʱ�������ٶȡ�·�̡�ʱ��֮��Ĺ�ϵʽ��ô𰸣�
��2���ֱ����ֱ��QR��MN�Ľ���ʽ�������ǹ��ɷ����鼴���������ʱ��ʱ�䣬�Ӷ���ü׳����ʱ������ϣ�
��3���֢ټ�����ǰ��10ǧ��ʱ�����ü���ʻ��·�̼�ȥ����ʻ��·�̵���10ǧ���г�������⼴�ɣ������ڼ�ǰ��10ǧ��ʱ����������ʻ��·�̼�ȥ����ʻ��·�̵���10ǧ���г�������⼴�ɣ�
��� �⣺��1����ͼ��֪���׳���1Сʱ��ʻ��20ǧ�ף�֮��ʱ��Ϊ3Сʱ��·��Ϊ30ǧ�ף�
֮��ʱ��Ϊ3Сʱ���ٶ��ǣ���50-20���£�5-2��=10ǧ��/ʱ����
����ʻ���ٶ��ǣ�50��1=50ǧ��/ʱ��
�ʴ�Ϊ��20��10ǧ��/ʱ��50ǧ��/ʱ��
��2����ֱ��QR�Ľ���ʽΪy=ax+b���Ҿ�����2��20������5��50����
��$\left\{\begin{array}{l}{2a+b=20}\\{5a+b=50}\end{array}\right.$�����$\left\{\begin{array}{l}{a=10}\\{b=0}\end{array}\right.$��
��ֱ��QR�Ľ���ʽΪy=10x��2��2��5����
��ֱ��MN�Ľ���ʽΪy=mx+n���Ҿ�����2��0������3��50����
��$\left\{\begin{array}{l}{2m+n=0}\\{3m+n=50}\end{array}\right.$�����$\left\{\begin{array}{l}{m=50}\\{n=-100}\end{array}\right.$��
��ֱ��MN�Ľ���ʽΪy=50x-100��
��$\left\{\begin{array}{l}{y=10x}\\{y=50x-100}\end{array}\right.$��x=2.5��
2.5-1=1.5��ʱ��
��׳���1.5�����ϣ�
��3�����ҳ���xСʱ������10ǧ�ף�
��������ǰ��10ǧ��ʱ��10x+20-50x=10�����x=$\frac{1}{4}$��
2+$\frac{1}{4}$=2$\frac{1}{4}$��ʱ����
�����ڼ�ǰ��10ǧ��ʱ��50x-��10x+20��=10�����x=$\frac{3}{4}$��
2+$\frac{3}{4}$=2$\frac{3}{4}$��ʱ����
��2$\frac{1}{4}$ʱ��2$\frac{3}{4}$ʱ�������10ǧ�ף�
���� ���⿼����һ�κ�����Ӧ�ã�����ѧ���۲�ͼ������������������е��⣮

 Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д� �Ľ���ǣ�������
�Ľ���ǣ�������