题目内容
【题目】如图,正五边形ABCDE的边长为2,连结AC、AD、BE,BE分别与AC和AD相交于点F、G,连结DF,给出下列结论:①∠FDG=18°;②FG=3﹣ ![]() ;③(S四边形CDEF)2=9+2
;③(S四边形CDEF)2=9+2 ![]() ;④DF2﹣DG2=7﹣2
;④DF2﹣DG2=7﹣2 ![]() .其中结论正确的个数是( )
.其中结论正确的个数是( )
A.1
B.2
C.3
D.4
【答案】B
【解析】解:①∵五方形ABCDE是正五边形,
∴AB=BC,∠ABC=180°﹣ ![]() =108°,
=108°,
∴∠BAC=∠ACB=36°,
∴∠ACD=108°﹣36°=72°,
同理得:∠ADE=36°,
∵∠BAE=108°,AB=AE,
∴∠ABE=36°,
∴∠CBF=108°﹣36°=72°,
∴BC=FC,
∵BC=CD,
∴CD=CF,
∴∠CDF=∠CFD= ![]() =54°,
=54°,
∴∠FDG=∠CDE﹣∠CDF﹣∠ADE=108°﹣54°﹣36°=18°;
所以①正确;
②∵∠ABE=∠ACB=36°,∠BAC=∠BAF,
∴△ABF∽△ACB,
∴ ![]() ,
,
∴ABED=ACEG,
∵AB=ED=2,AC=BE=BG+EF﹣FG=2AB﹣FG=4﹣FG,EG=BG﹣FG=2﹣FG,
∴22=(2﹣FG)(4﹣FG),
∴FG=3+ ![]() >2(舍),FG=3﹣
>2(舍),FG=3﹣ ![]() ;
;
所以②正确;
③如图1,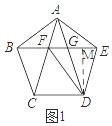
∵∠EBC=72°,∠BCD=108°,
∴∠EBC+∠BCD=180°,
∴EF∥CD,
∵EF=CD=2,
∴四边形CDEF是平行四边形,
过D作DM⊥EG于M,
∵DG=DE,
∴EM=MG= ![]() EG=
EG= ![]() (EF﹣FG)=
(EF﹣FG)= ![]() (2﹣3+
(2﹣3+ ![]() )=
)= ![]() ,
,
由勾股定理得:DM= ![]() =
= ![]() =
= ![]() ,
,
∴(S四边形CDEF)2=EF2DM2=4× ![]() =10+2
=10+2 ![]() ;
;
所以③不正确;
④如图2,连接EC,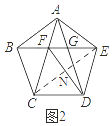
∵EF=ED,
∴CDEF是菱形,
∴FD⊥EC,
∵EC=BE=4﹣FG=4﹣(3﹣ ![]() )=1+
)=1+ ![]() ,
,
∴S四边形CDEF= ![]() FDEC=2×
FDEC=2× ![]() ,
,![]() ×FD×(1+
×FD×(1+ ![]() )=
)= ![]() ,
,
FD2=10﹣2 ![]() ,
,
∴DF2﹣DG2=10﹣2 ![]() ﹣4=6﹣2
﹣4=6﹣2 ![]() ,
,
所以④不正确;
本题正确的有两个,
故答案为:B.
①根据正五边形的性质证明△ABC,△ABE,△ADE是等腰三角形,求出∠ABC,∠ACB,∠BCD,∠CDE及∠ADE的度数,再证明CD=CF,根据等边对等角得出∠CDF=∠CFD=54°,然后根据∠FDG=∠CDE﹣∠CDF﹣∠ADE,计算即可求出∠FDG的度数,可对①作出判断;②先利用相似三角形的判定证明△ABF∽△ACB,得出ABED=ACEG,建立方程求出FG的长,就可对②作出判断;③先根据已知证明四边形CDEF是平行四边形,过D作DM⊥EG于M,求出EM的长,再利用勾股定理求出DM的长,然后求出(S四边形CDEF)2的值,可对③作出判断;④根据菱形的判断方法证明CDEF是菱形,得出FD⊥EC,求出EC的长,再根据菱形的面积公式建立方程求出FD2的长,然后求出DF2﹣DG2即可,就可对④作出判断;即可得出答案。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案