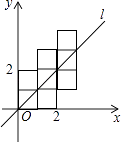题目内容
【题目】如图,已知,线段![]() 直线
直线![]() ,垂足为
,垂足为![]() ,平移线段
,平移线段![]() ,使点
,使点![]() 与点
与点![]() 重合,点
重合,点![]() 的对应点记为点
的对应点记为点![]() .
.

操作与思考:
(1)画出线段![]() 和直线
和直线![]() ;
;
(2)直线![]() 与
与![]() 的位置关系是_______,理由是:____________________________;
的位置关系是_______,理由是:____________________________;
线段![]() 与
与![]() 的数量关系是_______,理由是:____________________________.
的数量关系是_______,理由是:____________________________.
实践与应用:
(3)如图,等边![]() 和等边
和等边![]() 的面积分别为3和5,点
的面积分别为3和5,点![]() 、
、![]() 、
、![]() 在一直线上,则
在一直线上,则![]() 的面积是_____________.
的面积是_____________.

(4)如图,网格中每个小正方形的边长为1,请用三种不同方法,求出![]() 的面积.
的面积.

【答案】(1)见解析;(2)![]() ,理由见解析;
,理由见解析;![]() ,理由见解析;(3)5;(4)见解析.
,理由见解析;(3)5;(4)见解析.
【解析】
(1)根据平移的性质及线段、直线的含义画图即可;
(2)根据平移的性质解答即可;
(3)根据两平行线间的距离相等及三角形的面积公式求解即可;
(4)分别用补法、割法及两平行线间的距离相等求解即可.
操作与思考:
(1)画线段![]() 和直线
和直线![]() ;
;
(2)![]() 理由:两组对应点的连线平行(或在同一条直线上);
理由:两组对应点的连线平行(或在同一条直线上);
(3)![]() , 理由:平移不改变图形的大小;
, 理由:平移不改变图形的大小;

实践与应用:
(3)∵△ABC与△DCE都是等边三角形,
∴∠ACB=∠DEC=60°,
∴AC∥DE,
∴![]() ;
;
(4)方法1:![]() ;
;
方法2:![]() ;
;
方法3:∵![]() ,
,
∴![]() .
.


练习册系列答案
相关题目