Question

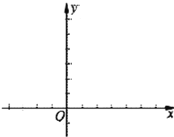
【题目】如图，在函数y1=（x＜0）和y2=（x＞0）的图象上，分别有A、B两点，若AB∥x轴，交y轴于点C，且OA⊥OB，S△AOC=，S△BOC=，则线段AB的长度=__．

Answer 1

【答案】

【解析】

已知S△AOC=，S△BOC=，根据反比例函数k的几何意义可得k1=﹣1，k2=9，即可得两反比例解析式为y=﹣，y=；设B点坐标为（，t）（t＞0），由AB∥x轴，可得A点的纵坐标为t，代入y=﹣求得A点坐标为（﹣，t）；再证明Rt△AOC∽Rt△OBC，根据相似三角形的性质可得OC：BC=AC：OC，代入数据可得t： =：t，解得t=，由此可得A点坐标为（﹣，），B点坐标为（3，），即可求得线段AB的长度．

∵S△AOC=，S△BOC=，

∴|k1|=， |k2|=，

∴k1=﹣1，k2=9，

∴两反比例解析式为y=﹣，y=，

设B点坐标为（，t）（t＞0），

∵AB∥x轴，

∴A点的纵坐标为t，

把y=t代入y=﹣得x=﹣，

∴A点坐标为（﹣，t），

∵OA⊥OB，

∴∠AOC=∠OBC，

∴Rt△AOC∽Rt△OBC，

∴OC：BC=AC：OC，即t： =：t，

∴t=，

∴A点坐标为（﹣，），B点坐标为（3，），

∴线段AB的长度=3﹣（﹣）=．

故答案为：．