题目内容
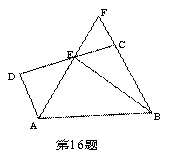
如图1是由两块全等的含30°角的直角三角板摆放而成,斜边AC=10.
(1)若将△ADE沿直线AE翻折到如图2的位置,ED'与BC交于点F,求证:CF=EF;
(2)求EF的长;
(3)将图2中的△AD'E沿直线AE向右平移到图3的位置,使D'点落在BC上,求出平移的距离.
(1)证明:∵△ABC≌△ADE,
∴AC=AE,AB=AD,
根据翻折对称性,AD′=AD,
∴AD′=AB,
∴AC-AD′=AE-AB,
即CD′=BE,
在△CD′F与△EBF中,
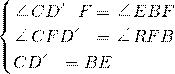
∴△CD′F≌△EBF(AAS),
∴CF=EF(全等三角形对应边相等);
(2)解:∵∠C=30°,AC=10,
∴AB=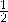 AC=
AC=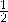 ×10=5,
×10=5,
∴EB=10-AB=5,
在△EFB中,∠FEB=30°,
∴BF=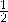 EF,
EF,
根据勾股定理得EF2=BF2+EB2,
∴EF2=(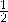 EF)2+52,
EF)2+52,
解得EF=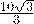 ;
;
(3)解:根据平移,D′D″∥AB,
又∵AD′=AB=5,CD′=10-AD′=5,
∴D′D″是△ABC的中位线,
∵∠C=30°,AC=10,
∴D′D″=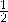 AB=
AB=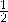 ×
×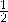 AC=
AC=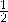 ×
×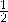 ×10=
×10= ,
,
故平移距离 .
.

 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案为了解初三学生的体育锻炼时间,小华调查了某班45名同学一周参加体育锻炼的情况,并把它绘制成折线统计图.那么关于该班45名同学一周参加体育锻炼时
|
A.众数是9 B.中位数是9
C.平均数是9 D.锻炼时间不低于9小时的有14人

 为:
为: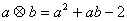 ,有下列命题:
,有下列命题: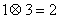 ;
;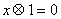 的根为:
的根为: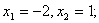
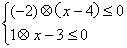 的解集为
的解集为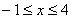
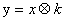 的图像与坐标轴交点组成的三角形面积为3,则此函数的顶点坐标是
的图像与坐标轴交点组成的三角形面积为3,则此函数的顶点坐标是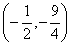 其中正确的( )
其中正确的( ) 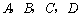 和一个算式.将这四张卡片背面向上洗匀,从中随机抽取一张,记录字母后放回,重新洗匀再从中随机抽取一张,记录字母.
和一个算式.将这四张卡片背面向上洗匀,从中随机抽取一张,记录字母后放回,重新洗匀再从中随机抽取一张,记录字母.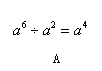
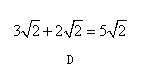
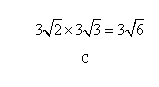

 (
(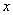 为未知数)无解,则函数
为未知数)无解,则函数 图象与
图象与 +
+ =-2 B.
=-2 B.
 =
=
 =2
=2