题目内容
在Rt△ABC中,∠BCA=90°,CD是高,已知Rt△ABC的三边长都是整数,且BD=113,则Rt△BCD与Rt△ACD的周长之比是 .
考点:三角形边角关系
专题:
分析:根据题意易证△BCD∽△BAC,利用相似三角形的性质及勾股定理列式,解方程组即可解答.
解答:解:如图,设BC=a,CA=b,AB=c,
∵Rt△BCD∽Rt△BAC,
∴
=
,即BC2=BD•BA,
∴a2=113c.
因a2为完全平方数,且11是质数,
∴c为11的倍数,令c=11k2(k为正整数),则a=112k,
于是由勾股定理得b=
=11k
,又因为b为整数,
∴k2-112是完全平方数,令k2-112=m2,则(k+m)(k-m)=112,
∵(k+m)>(k-m)>0且11为质数,
∴
,解得
,于是a=112×61,b=11×61×60,
又∵Rt△BCD∽Rt△CAD,
∴它们周长的比等于它们的相似比.
即
=
=
,
故答案为:
.

∵Rt△BCD∽Rt△BAC,
∴
| BC |
| BA |
| BD |
| BC |
∴a2=113c.
因a2为完全平方数,且11是质数,
∴c为11的倍数,令c=11k2(k为正整数),则a=112k,
于是由勾股定理得b=
| c2-a2 |
| k2-112 |
∴k2-112是完全平方数,令k2-112=m2,则(k+m)(k-m)=112,
∵(k+m)>(k-m)>0且11为质数,
∴
|
|
又∵Rt△BCD∽Rt△CAD,
∴它们周长的比等于它们的相似比.
即
| a |
| b |
| 112×61 |
| 11×61×60 |
| 11 |
| 60 |
故答案为:
| 11 |
| 60 |
点评:本题考查了三角形的边角关系.解答此题是要根据题意列出方程,把解三角形转化成解方程的形式解答.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
设M=3n+2×17n,其中n为正整数,则下列结论正确的是( )
| A、有且只有一个n,使得M为完全平方数 |
| B、存在多于一个的有限个n,使得M为完全平方数 |
| C、存在无数个n,使得M为完全平方数 |
| D、不存在n,使得M为完全平方数 |
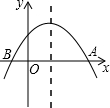 如图,已知抛物线y=x2+bx+c与坐标轴交于A、B两点,则一元二次方程x2+bx+c=0的根的情况是( )
如图,已知抛物线y=x2+bx+c与坐标轴交于A、B两点,则一元二次方程x2+bx+c=0的根的情况是( )| A、没有实数根 |
| B、有两个相等的实数根 |
| C、有两个不相等的实数根 |
| D、可能有实数根,也可能没有实数根 |